题目内容
平面直角坐标系中,三角形ABC的三个顶点A(-3,0)、B(2,1)、C(-2,3),写出下列直线的一般式方程.(1)BC边上中线AD;
(2)BC边的垂直平分线DE.
【答案】分析:(1)根据中点坐标公式求出B与C的中点D的坐标,利用A和D的坐标写出中线方程即可;
(2)求出直线BC的斜率,然后根据两直线垂直时斜率乘积为-1求出BC垂直平分线的斜率,由(1)中D的坐标,写出直线DE的方程即可.
解答:解:(1)设BC中点D的坐标为(x,y),
因为B(2,1)、C(-2,3),
所以x=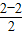 =0,y=
=0,y=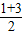 =2.
=2.
因为BC边的中线AD过点A(-3,0),D(0,2)两点,
所以由截距式得AD所在直线方程为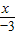 +
+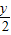 =1,即2x-3y+6=0.
=1,即2x-3y+6=0.
(2)由题意可得:BC的斜率k1=- ,
,
所以BC的垂直平分线DE的斜率k2=2,
由斜截式得直线DE的方程为y=2x+2.
点评:考查学生会根据一点和斜率或两点坐标写出直线的方程,掌握两直线垂直时斜率的关系.会利用中点坐标公式求线段的中点坐标.
(2)求出直线BC的斜率,然后根据两直线垂直时斜率乘积为-1求出BC垂直平分线的斜率,由(1)中D的坐标,写出直线DE的方程即可.
解答:解:(1)设BC中点D的坐标为(x,y),
因为B(2,1)、C(-2,3),
所以x=
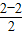 =0,y=
=0,y=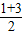 =2.
=2.因为BC边的中线AD过点A(-3,0),D(0,2)两点,
所以由截距式得AD所在直线方程为
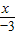 +
+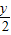 =1,即2x-3y+6=0.
=1,即2x-3y+6=0.(2)由题意可得:BC的斜率k1=-
 ,
,所以BC的垂直平分线DE的斜率k2=2,
由斜截式得直线DE的方程为y=2x+2.
点评:考查学生会根据一点和斜率或两点坐标写出直线的方程,掌握两直线垂直时斜率的关系.会利用中点坐标公式求线段的中点坐标.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 三个顶点的坐标为A(a,0),B(0,b),C(0,c),点D(d,0)在线段OA上(异于端点),设a,b,c,d均为非零实数,直线BD交AC于点E,则OE所在的直线方程为 _
三个顶点的坐标为A(a,0),B(0,b),C(0,c),点D(d,0)在线段OA上(异于端点),设a,b,c,d均为非零实数,直线BD交AC于点E,则OE所在的直线方程为 _