题目内容
现有60件产品,编号从1到60,若用系统抽样方法从中抽取6件检验,则所抽到的个体编号可能是
| A.5,10,15,20,25,30 | B.2,14,26,28,42,56 |
| C.5,8,31,36,48,54 | D.3,13,23,33,43,53 |
D
解析试题分析:根据系统抽样方法,按照一定的规则抽取样本。通常是将l加上间隔k得到第二个个体编号(l+k),再加k得到第3个个体编号(l+2k),依次进行下去,直到获得整个样本。
本题分6组,每组10 件产品,所以,所抽到的个体编号可能是3,13,23,33,43,53,选D。
考点:本题主要考查系统抽样方法。
点评:简单题,注意,根据系统抽样方法,按照一定的规则抽取样本。通常是将l加上间隔k得到第二个个体编号(l+k),再加k得到第3个个体编号(l+2k),依次进行下去,直到获得整个样本。

练习册系列答案
相关题目
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
| A.y=-10x+200 | B.y=10x+200 |
| C.y=-10x-200 | D.y=10x-200 |
为了了解某地区高三学生的身体素质情况,抽查了该地区 名年龄为17.5岁-18岁的男生体重(
名年龄为17.5岁-18岁的男生体重( ) ,得到频率分布直方图如下
) ,得到频率分布直方图如下
根据上图可得这 名学生中体重在[56.5,64.5]的学生人数是( )
名学生中体重在[56.5,64.5]的学生人数是( )
A. | B.30 | C. | D.50 |
如果数据 、
、 、……
、…… 的平均值为
的平均值为 ,方差为
,方差为 ,则
,则 ,
, ,……
,……  的平均值和方差分别为( )
的平均值和方差分别为( )
A. 和 和 | B.3 +5和9 +5和9 |
C.3 +5和 +5和 | D.3 +5 和9 +5 和9 +30 +30 +25 +25 |
某交警部门对城区上下班交通情况作抽样调查,上下班时间各抽取12辆机动车的行驶速度(单位:km/h)作为样本进行研究,做出样本的茎叶图,则上班、下班时间行驶速度的中位数分别是( )
| A.28 27.5 | B.28 28.5 |
| C.29 27.5 | D.29 28.5 |
对变量x,y观测数据(x1,y1)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(u1,v1)(i=1,2,…,10),得散点图2.由这两个散点图可以判断.( )
| A.变量x与y正相关,u与v正相关 |
| B.变量x与y正相关,u与v负相关 |
| C.变量x与y负相关,u与v正相关 |
| D.变量x与y负相关,u与v负相关 |
若样本 +2,
+2, +2, ,
+2, , +2的平均数为10,方差为3,则样本2
+2的平均数为10,方差为3,则样本2 +3,2
+3,2 +3,… ,2
+3,… ,2 +3,
+3,
的平均数、方差、标准差是( )
A.19,12, | B.23,12, | C.23,18, | D.19,18, |
 )负相关,则其回归方程可能是( )
)负相关,则其回归方程可能是( ) B.
B. C.
C.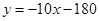 D
D 
 =bx+a必过( )
=bx+a必过( ) B.点
B.点 C.点
C.点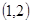 D.点
D.点