题目内容
(本小题满分12分)
已知椭圆方程为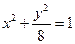 ,射线
,射线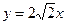 (x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(Ⅰ)求证直线AB的斜率为定值;
(Ⅱ)求△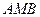 面积的最大值.
面积的最大值.
已知椭圆方程为
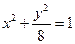 ,射线
,射线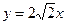 (x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).(Ⅰ)求证直线AB的斜率为定值;
(Ⅱ)求△
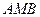 面积的最大值.
面积的最大值.(Ⅰ)∵斜率k存在,不妨设k>0,求出M(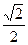 ,2).-------------------------------1分
,2).-------------------------------1分
直线MA方程为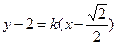 ,
,
分别与椭圆方程联立,可解出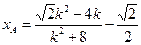 ,----------------------------3分
,----------------------------3分
同理得,直线MB方程为 .
.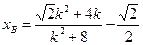 -------4分
-------4分
∴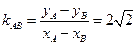 ,为定值.----------------------------------------------------6分
,为定值.----------------------------------------------------6分
(Ⅱ)设直线AB方程为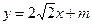 ,与
,与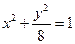 联立,消去y得
联立,消去y得

 .----------- -----------------------------7分
.----------- -----------------------------7分
由 >0得一4<m<4,且m≠0,
>0得一4<m<4,且m≠0,
点M到AB的距离为 .------------------------------------------------------8分
.------------------------------------------------------8分
 ---9分
---9分
设△AMB的面积为S. ∴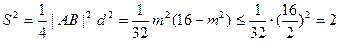 .
.
当 时,得
时,得 .--------------------------------------------------------------12分
.--------------------------------------------------------------12分
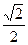 ,2).-------------------------------1分
,2).-------------------------------1分直线MA方程为
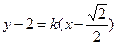 ,
,分别与椭圆方程联立,可解出
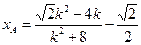 ,----------------------------3分
,----------------------------3分同理得,直线MB方程为
 .
.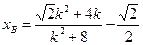 -------4分
-------4分∴
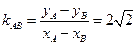 ,为定值.----------------------------------------------------6分
,为定值.----------------------------------------------------6分(Ⅱ)设直线AB方程为
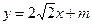 ,与
,与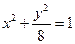 联立,消去y得
联立,消去y得
 .----------- -----------------------------7分
.----------- -----------------------------7分由
 >0得一4<m<4,且m≠0,
>0得一4<m<4,且m≠0,点M到AB的距离为
 .------------------------------------------------------8分
.------------------------------------------------------8分 ---9分
---9分设△AMB的面积为S. ∴
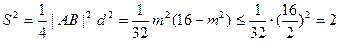 .
.当
 时,得
时,得 .--------------------------------------------------------------12分
.--------------------------------------------------------------12分略

练习册系列答案
相关题目
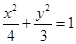 内有一点
内有一点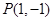 ,
,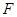 为椭圆的右焦点,在椭圆上有一点
为椭圆的右焦点,在椭圆上有一点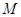 ,
,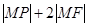 的值最小,则此最小值为 ( )
的值最小,则此最小值为 ( )



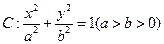 过点
过点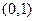 ,且离心率为
,且离心率为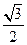 .
.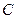 的方程;
的方程;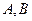 为椭圆
为椭圆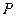 是椭圆
是椭圆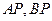 分别交直线
分别交直线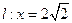 于
于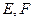 两点.证明:以线段
两点.证明:以线段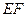 为直径的圆恒过
为直径的圆恒过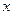 轴上的定点.
轴上的定点. 中,
中, ,
, ,
, ,则
,则 ( )
( )



 的焦点坐标是
的焦点坐标是 

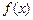 =
=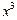 +
+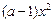 +3x+b的图象与x轴有三个不同交点,且交点的横坐标分别可作为抛物线、双曲线、椭圆的离心率,则实数a的取值范围是 .
+3x+b的图象与x轴有三个不同交点,且交点的横坐标分别可作为抛物线、双曲线、椭圆的离心率,则实数a的取值范围是 .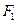 、
、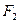 分别是椭圆
分别是椭圆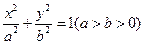 的左、右焦点,点B是其上顶点,椭圆的右准线与
的左、右焦点,点B是其上顶点,椭圆的右准线与
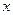 轴交于点N,且
轴交于点N,且 。
。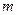 :
: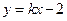 与椭圆交于不同的两点M、Q,若△BMQ是以MQ为底边的等腰三角形,求
与椭圆交于不同的两点M、Q,若△BMQ是以MQ为底边的等腰三角形,求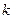 的值。
的值。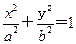 (a>b>0)的离心率e=
(a>b>0)的离心率e=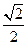 ,左、右焦点分别为F1、F2,点P(2,
,左、右焦点分别为F1、F2,点P(2,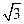 ),点F2在线段PF1的中垂线上
),点F2在线段PF1的中垂线上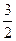 ,0)且互相垂直的两条直线,l1交E于A,
,0)且互相垂直的两条直线,l1交E于A, B两点,l2交E于C,D两点,求l1的斜率k的取值范围;
B两点,l2交E于C,D两点,求l1的斜率k的取值范围; ,求出该定点坐标;若不经过,请说明理由。
,求出该定点坐标;若不经过,请说明理由。