题目内容
已知梯形的两对角线分别为a和b，且它们的夹角为60°，那么该梯形的面积为
- A.
ab - B.
ab - C.
ab - D.
ab
B
分析：设梯形ABCD，对角线AC和BD相交于O，AC=a，BD=b，过C作CE∥BD，交AB延长线于E，则∠BOC=60°，则四边形ABEC是平行四边形，根据S梯形ABCD=S△ACE即可求出答案．
解答：设梯形ABCD，对角线AC和BD相交于O，AC=a，BD=b，
过C作CE∥BD，交AB延长线于E，则∠BOC=60°，则四边形BECD是平行四边形，
∴∠ACE=120°，∴CE=BD，
∵S△BCE=S△BCD=S△ACD，
故S梯形ABCD=S△ACE=
AC•CE•sin120°=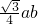
，
故选B．
点评：本题考查了梯形的性质，三角形中的几何计算，关键是正确地作辅助线进行解题，属于中档题．
分析：设梯形ABCD，对角线AC和BD相交于O，AC=a，BD=b，过C作CE∥BD，交AB延长线于E，则∠BOC=60°，则四边形ABEC是平行四边形，根据S梯形ABCD=S△ACE即可求出答案．
解答：设梯形ABCD，对角线AC和BD相交于O，AC=a，BD=b，
过C作CE∥BD，交AB延长线于E，则∠BOC=60°，则四边形BECD是平行四边形，
∴∠ACE=120°，∴CE=BD，
∵S△BCE=S△BCD=S△ACD，
故S梯形ABCD=S△ACE=
AC•CE•sin120°=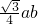，故选B．
点评：本题考查了梯形的性质，三角形中的几何计算，关键是正确地作辅助线进行解题，属于中档题．
练习册系列答案
相关题目
的两焦点分别为
，且椭圆上的点到
的最小距离为
.
作直线
交椭圆
两点，设线段
的中垂线交
轴于
，求m的取值范围.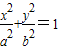
的两焦点分别为F1、F2，点P是以F1F2为直径的圆与椭圆的交点，若∠PF1F2=5∠PF2F1，则椭圆离心率为（ ）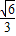
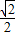
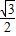
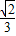
ab
ab
ab
ab