题目内容
已知抛物线C1:y2=2px的准线经过双曲线C2: 的左焦点,若抛物线C1与双曲线C2的一个交点是
的左焦点,若抛物线C1与双曲线C2的一个交点是 .
.
(1)求抛物线C1的方程;
(2)求双曲线C2的方程.
解:(1)把交点 代入抛物线C1:y2=2px得
代入抛物线C1:y2=2px得 ,解得p=2,∴抛物线C1的方程是y2=4x.
,解得p=2,∴抛物线C1的方程是y2=4x.
(2)∵抛物线y2=4x的准线方程是x=-1,
∴双曲线C2: 的左焦点是(-1,0).
的左焦点是(-1,0).
设双曲线C2的方程为 ,
,
把交点 代入,得
代入,得 ,整理得9a4-37a2+4=0.
,整理得9a4-37a2+4=0.
解得 ,或a2=4(舍去).
,或a2=4(舍去).
∴ .
.
∴双曲线C2的方程是 .
.
分析:(1)把交点 代入抛物线C1:y2=2px,就能得到抛物线C1的方程.
代入抛物线C1:y2=2px,就能得到抛物线C1的方程.
(2)求出抛物线C1的准线方程,得到双曲线C2的左焦点,然后设出双曲线的标准方程,把交点M代入,可以求出双曲线C2的方程.
点评:第(1)题比较简单,把交点M代入y2=2px就能求出抛物线C1的方程,第(2)题在第一题的基础上得到双曲线C2的左焦点,知道焦点坐标后,双曲线方程通常设为 .
.
 代入抛物线C1:y2=2px得
代入抛物线C1:y2=2px得 ,解得p=2,∴抛物线C1的方程是y2=4x.
,解得p=2,∴抛物线C1的方程是y2=4x.(2)∵抛物线y2=4x的准线方程是x=-1,
∴双曲线C2:
 的左焦点是(-1,0).
的左焦点是(-1,0).设双曲线C2的方程为
 ,
,把交点
 代入,得
代入,得 ,整理得9a4-37a2+4=0.
,整理得9a4-37a2+4=0.解得
 ,或a2=4(舍去).
,或a2=4(舍去).∴
 .
.∴双曲线C2的方程是
 .
.分析:(1)把交点
 代入抛物线C1:y2=2px,就能得到抛物线C1的方程.
代入抛物线C1:y2=2px,就能得到抛物线C1的方程.(2)求出抛物线C1的准线方程,得到双曲线C2的左焦点,然后设出双曲线的标准方程,把交点M代入,可以求出双曲线C2的方程.
点评:第(1)题比较简单,把交点M代入y2=2px就能求出抛物线C1的方程,第(2)题在第一题的基础上得到双曲线C2的左焦点,知道焦点坐标后,双曲线方程通常设为
 .
. 
练习册系列答案
相关题目
 (2012•河北模拟)已知抛物线C1:y2=2px和圆
(2012•河北模拟)已知抛物线C1:y2=2px和圆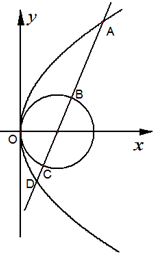 已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).
已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).