题目内容
设函数 定义在R上,对任意实数m、n,恒有
定义在R上,对任意实数m、n,恒有 且当
且当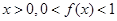
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上递减。
【答案】
略
【解析】(1)证明:在f(m+n)=f(m)f(n)中,
令m=1,n=0,得f(1)=f(1)f(0).
∵0<f(1)<1,∴f(0)=1…………………2分
设x<0,则-x>0.令m=x,n=-x,代入条件式有f(0)=f(x)·f(-x),而f(0)=1,
∴f(x)= >1……………………….6分
>1……………………….6分
(2)证明:设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1………………….8分
令m=x1,m+n=x2,则n=x2-x1,代入条件式,得f(x2)=f(x1)·f(x2-x1),…10分
即0< <1.∴f(x2)<f(x1)……………….12分
<1.∴f(x2)<f(x1)……………….12分
∴f(x)在R上单调递减………………….14分

练习册系列答案
相关题目
 是定义在R上的周期函数,周期为
是定义在R上的周期函数,周期为 ,对
,对 都有
都有 ,且当
,且当 时,
时, ,若在区间
,若在区间 内关于x的方程
内关于x的方程 =0
=0 恰有3个不同的实根,则a的取值范围是( )
恰有3个不同的实根,则a的取值范围是( ) C.
C. D.
D.
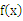 是定义在R上的奇函数,且当x
是定义在R上的奇函数,且当x 时,
时, ,若对任意的
,若对任意的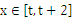 ,不等式
,不等式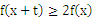 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( ) B.
B. C.
C. D.
D. 
 是定义在R上的奇函数,对任意
是定义在R上的奇函数,对任意 都有
都有 ,
, 时,
时, ,则
,则
 是定义在R上的奇函数,且对任意a、b
是定义在R上的奇函数,且对任意a、b ,当
,当 时,都有
时,都有 .
. ,试比较
,试比较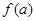 与
与 的大小关系;
的大小关系; 对任意
对任意 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.