题目内容
20．已知点M（1，2），N（4，3），动点P满足$\overrightarrow{OP}$=λ$\overrightarrow{OM}$+μ$\overrightarrow{ON}$，其中O为坐标原点，且λμ≥0，|λ+μ|≤1，则点P所在平面区域的面积为5．分析 当λ，μ均大于0时，P点所在区域为△OMN内部，当λ，μ均小于0时，P点所在区域为△OMN关于原点对称的三角形．
解答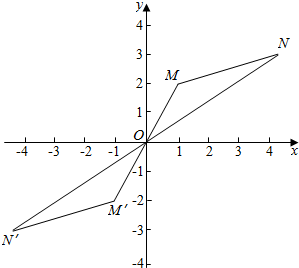 
解：当λ＞0，μ＞0，0≤λ+μ≤1时，点P所在区域为△OMN内部（含边界），
当λ＜0，μ＜0，-1≤λ+μ≤0时，点P所在区域为△OMN内部（含边界）关于原点得对称区域．
|$\overrightarrow{OM}$|=$\sqrt{5}$，|$\overrightarrow{ON}$|=5，$\overrightarrow{OM}•\overrightarrow{ON}$=10，
∴cos＜$\overrightarrow{OM}$，$\overrightarrow{ON}$＞=$\frac{10}{5\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$，
∴sin＜$\overrightarrow{OM}$，$\overrightarrow{ON}$＞=$\frac{\sqrt{5}}{5}$．
∴S△OMN=$\frac{1}{2}×$5×$\sqrt{5}$×$\frac{\sqrt{5}}{5}$=$\frac{5}{2}$．
∴点P所在的区域面积S=2S△OMN=5．
故答案为：5．
点评 本题考查了平面向量的基本定理及其意义，属于基础题．
练习册系列答案
相关题目
11．若直线x+my-2=0的倾斜角为30°，则实数m的值是（ ）
| A． | -$\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | -$\sqrt{3}$ | D． | $\sqrt{3}$ |
8．根据上海高考改革方案，2017年，高中生可从思想政治、历史、地理、物理、化学、生命科学6门学业考试科目中选3门参加等级性考试，并且这3门学业考试科目等级考试成绩将这算，计入高考总分，上海37所本科高校，从目前公布的1096个专业（类）的选考科目老看，学生选考物理可以满足1070个专业选科要求，覆盖率97.63%；选考化学可以满足992个专业选科要求，覆盖率为90.51%；选考生命科学可以满足877个专业选科要求，覆盖率为80.02%，地理、历史、思想政治的覆盖率分别为64.05%、63.5%、62.14%，为了进一步调查学生选考的意向，某机构对本市两所学校各100名高一新生进行了选考调查，且规定从6门学业考试中每一位学生只能选择1门，结果如下：
（1）分别计算甲乙两校选考理科专业的频率，若将该频率视为概率，求从乙校高一新生中随机选取3人，其中恰有2人选考理科专业的概率；
（2）若从甲校高一新生中任取1人，从乙校高一新生中任取2人，记3人中选考理科专业的人数为随机变量X，求X的分布列和数学期望．
| 物理 | 化学 | 生命科学 | 政治 | 历史 | 地理 | |
| 甲校 | 35 | 20 | 15 | 7 | 8 | 15 |
| 乙校 | 30 | 14 | 16 | 11 | 14 | 15 |
（2）若从甲校高一新生中任取1人，从乙校高一新生中任取2人，记3人中选考理科专业的人数为随机变量X，求X的分布列和数学期望．