题目内容
求过点P(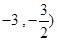 ,且被圆C:
,且被圆C: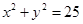 截得的弦长等于8的直线方程。
截得的弦长等于8的直线方程。
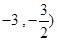 ,且被圆C:
,且被圆C: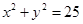 截得的弦长等于8的直线方程。
截得的弦长等于8的直线方程。 或
或
试题分析:已知直线过一点求直线方程,应分斜率存在和不存在两种情况,斜率不存在时单独验证,当斜率存在时设为点斜式,再利用弦心距半弦长和半径之间的勾股关系得到关于k的方程,解方程可得k值,进一步利用点斜式得直线方程.
若直线的斜率不存在即
 时,由
时,由 解得
解得 ,则弦长
,则弦长 符合题意。若直线的斜率存在时,设直线的方程:
符合题意。若直线的斜率存在时,设直线的方程: ,即
,即 .由题意可知弦心距为
.由题意可知弦心距为 ,所以
,所以 解得
解得 ,直线方程:
,直线方程: .综上所述:直线方程是
.综上所述:直线方程是  或
或

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
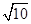 .
. 是半径等于
是半径等于 的圆
的圆 的直径,
的直径, 是圆
是圆 ,
, ,若
,若 ,
, ,则
,则 .
.
 与直线
与直线 有两个交点,则
有两个交点,则 的取值范围是__________________.
的取值范围是__________________. 与圆
与圆 有公共点,则 ( )
有公共点,则 ( )



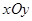 中,点
中,点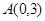 ,直线
,直线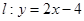 .设圆
.设圆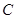 的半径为
的半径为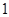 ,圆心在
,圆心在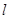 上.
上.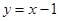 上,过点
上,过点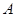 作圆
作圆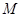 ,使
,使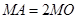 ,求圆心
,求圆心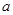 的取值范围.
的取值范围.
 中,已知点
中,已知点 在圆
在圆 内,动直线
内,动直线 过点
过点 且交圆
且交圆 于
于 两点,若△ABC的面积的最大值为
两点,若△ABC的面积的最大值为 ,则实数
,则实数 的取值范围为 .
的取值范围为 .