题目内容
等腰直角三角形ABC中，∠BAC=90°.若P、Q为斜边BC的三等分点，则tan∠PAQ=____________.解析：如图，建立直角坐标系.
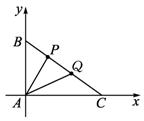
设AB=AC=3a,则P(a,2a),Q(2a,a),
∴tan∠PAQ=tan(∠PAC-∠QAC)
=
=
=
.
答案：
练习册系列答案
相关题目
在等腰直角三角形ABC中，过直角顶点C在∠ACB内部任作一射线CM，与线段AB交于点M，求AM＜AC的概率．等腰直角三角形ABC，E、F分别是斜边BC的三等分点，则tan∠EAF=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
题目内容
等腰直角三角形ABC中，∠BAC=90°.若P、Q为斜边BC的三等分点，则tan∠PAQ=____________.解析：如图，建立直角坐标系.
设AB=AC=3a,则P(a,2a),Q(2a,a),
∴tan∠PAQ=tan(∠PAC-∠QAC)
===.
答案：
A、
| ||||
B、
| ||||
C、
| ||||
D、
|