题目内容
(2007•武汉模拟)直线x-2y-2=0与曲线
(其中s为参数)交于A、B两点,点M 是线段AB的中点,则点M到y轴的距离是
|
10
10
.分析:欲求点M到y轴的距离,只需求出点M的横坐标,因为M点是线段AB的中点,所以M点的横坐标是A,B横坐标之和的
,只需联立直线与曲线方程,解出x1+x2即可.
| 1 |
| 2 |
解答:解:曲线
消去参数s,得,x=
+1,
设A、B两点坐标分别为(x1,y1),(x2,y2),
由
,得,y2-8y+4=0
∴y1+y2=8,x1+x2=2(y1+y2)+4=20
∴线 段AB的中点M的坐标为(10,4)
∴点M到y轴的距离是10
故答案为:10.
|
| y2 |
| 4 |
设A、B两点坐标分别为(x1,y1),(x2,y2),
由
|
∴y1+y2=8,x1+x2=2(y1+y2)+4=20
∴线 段AB的中点M的坐标为(10,4)
∴点M到y轴的距离是10
故答案为:10.
点评:本题主要考查了直线与抛物线交点的求法,以及中点坐标公式的应用,

练习册系列答案
相关题目
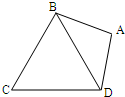 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=