题目内容
有一批材料可以建成长为20m的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形,问怎样设计,使围成的矩形的最大面积,最大面积是多少?
分析:设每个小矩形长为x,宽为y,则由题意可得4x+3y=20,列出矩形的面积公式,利用基本不等式,即可求得围成的矩形面积的最大值.
解答:解:设每个小矩形长为x,宽为y,
则有4x+3y=20,(0<x<5)
围成的矩形的面积S=3xy=x(20-4x)=4x(5-x)≤4(
)2=25,
当且仅当x=5-x,即x=
时,Smax=25(m2),
∴当围成的面积相等的小矩形的边长为
时,所围矩形面积的最大值为25m2.
则有4x+3y=20,(0<x<5)
围成的矩形的面积S=3xy=x(20-4x)=4x(5-x)≤4(
| x+5-x |
| 2 |
当且仅当x=5-x,即x=
| 5 |
| 2 |
∴当围成的面积相等的小矩形的边长为
| 5 |
| 2 |
点评:本题主要考查了函数的最值在实际生产生活中的应用.考查了学生运用所学知识解决实际问题的能力,设出自变量,将实际问题转化为函数模型是解答本题的关键.属于基础题.

练习册系列答案
相关题目
 17、有一批材料可以建成长为200m的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),则围成的矩形的最大面积是多少?
17、有一批材料可以建成长为200m的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),则围成的矩形的最大面积是多少?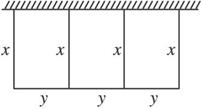
 (17) 有一批材料可以建成长为
(17) 有一批材料可以建成长为