题目内容
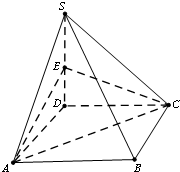 四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a.
四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a.(I)若M是底面ABCD的一个动点,且满足|MB|=|MS|,求点M在正方形ABCD内的轨迹;
(II)试问在线段SD上是否存在点E,使二面角C-AE-D的大小为60°?若存在,确定点E的位置;若不存在,请说明理由.
分析:由题设条件及图形,本题中出现了同一点出发的三个线段两两垂直,故可以建立空间坐标系,利用向量解决问题,以D为原点,
、
、
的方向分别为x、y、z轴的正方向建立空间直角坐标系,给出各点的坐标
(1)设M(x,y,0),则由|MB|=|MS|得
=
,整理即可得到点M在正方形ABCD内的轨迹;
(2)假设存在,设
=λ
(0≤λ≤1),
=(0,a,0)为平面ADE的一个法向量,设平面ACE的一个法向量为
=(x,y,z),用引入的参数λ表示出平面ACE的一个法向量为
,
再由二面角的大小是60°,建立方程求出参数λ的值,然后根据参数的值的范围确定出点E的位置,
| DA |
| DC |
| DS |
(1)设M(x,y,0),则由|MB|=|MS|得
| (x-a)2+(y-a)2 |
| x2+y2+a2 |
(2)假设存在,设
| DE |
| DS |
| DC |
| n |
| n |
再由二面角的大小是60°,建立方程求出参数λ的值,然后根据参数的值的范围确定出点E的位置,
解答:解:(1)以D为原点,
、
、
的方向分别为x、y、z轴的正方向建立空间直角坐标系,
则B(a,a,0),S(0,0,a),…(2分)
设M(x,y,0),则由|MB|=|MS|得
=
…(4分)
化简得x+y-
=0,所以点M在正方形ABCD内的轨迹为△ACD平行于边AC的中位线.…(6分)
(2)假设存在,设
=λ
(0≤λ≤1),
=(0,a,0)为平面ADE的一个法向量…(8分)
设平面ACE的一个法向量为
=(x,y,z),则
•
=0,
•
=0
即
,取z=1,得
=(λ,λ,1),…(10分)
所以cos600=
=
,又0≤λ≤1,解得λ=
,
故在线段SD上存在点E,
=
,使二面角C-AE-D的大小为600.…(13分)
| DA |
| DC |
| DS |
则B(a,a,0),S(0,0,a),…(2分)
设M(x,y,0),则由|MB|=|MS|得
| (x-a)2+(y-a)2 |
| x2+y2+a2 |
化简得x+y-
| a |
| 2 |
(2)假设存在,设
| DE |
| DS |
| DC |
设平面ACE的一个法向量为
| n |
| n |
| EA |
| n |
| EC |
即
|
| n |
所以cos600=
|
| ||||
|
|
| |λ| | ||
|
| ||
| 2 |
故在线段SD上存在点E,
| DE |
| ||
| 2 |
| DS |
点评:本题考查与二面角有关的立体几何证明题,解题的关键是熟练掌握二面角的平面角的做法以及用向量法求二面角的步骤,向量中的方程与立体几何中位置关系的对应,如数量积为0与垂直的对应,向量的共线与平行的对应,向量夹角与线线角,线面角,面面角的对应,本题考查了数形结合的思想,转化的思想,方程的思想,考查了待定系数建立方程的技巧,用向量解决立体几何问题的方法,本题知识性综合性强,考查空间想像能力,推理判断能力及转化的能力,本题运算量大,且多是符号运算,解题时要严谨.

练习册系列答案
相关题目
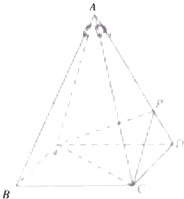 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的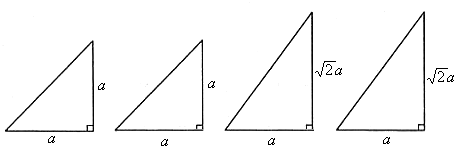
 (2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示.
(2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示. 如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=
如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=