题目内容
某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图：
（1）比较这两名队员在比赛中得分的均值和方差的大小；
（2）在甲队员的得分中任意抽取两个得分，求恰有一个得分超过14分的概率．
解：（1）由茎叶图可知：甲乙的平均值分别为
=
（9+7+11+12+14+16+23+28）=15，
=（7+8+10+15+17+19+21+23）=15，
故方差分别为：S2甲=[（9-15）2+（7-15）2+（11-15）2+（12-15）2+（14-15）2+（16-15）2+（23-15）2+（28-15）2]=45
S2乙=[（7-15）2+（8-15）2+（10-15）2+（15-15）2+（17-15）2+（19-15）2+（21-15）2+（23-15）2]=32.25
（2）从甲队员的8个得分中任取两个共有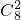
=32种方法，8个得分中有3个超过14分，5个不超过14分，
故恰有一个得分超过14分共有
=15种情况，
故所求的概率为P=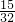
分析：（1）由茎叶图可的原始数据，代入平均值、方差得公式计算可得；
（2）总的加班时间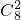=32种，符合条件的共=15种，由古典概型的概率公式可得答案．
点评：本题考查古典概型及其概率公式，涉及茎叶图和平均数和方差的求解，属基础题．
=（9+7+11+12+14+16+23+28）=15，=（7+8+10+15+17+19+21+23）=15，故方差分别为：S2甲=
[（9-15）2+（7-15）2+（11-15）2+（12-15）2+（14-15）2+（16-15）2+（23-15）2+（28-15）2]=45S2乙=
[（7-15）2+（8-15）2+（10-15）2+（15-15）2+（17-15）2+（19-15）2+（21-15）2+（23-15）2]=32.25（2）从甲队员的8个得分中任取两个共有
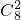=32种方法，8个得分中有3个超过14分，5个不超过14分，故恰有一个得分超过14分共有
=15种情况，故所求的概率为P=
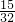
分析：（1）由茎叶图可的原始数据，代入平均值、方差得公式计算可得；
（2）总的加班时间
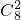=32种，符合条件的共=15种，由古典概型的概率公式可得答案．点评：本题考查古典概型及其概率公式，涉及茎叶图和平均数和方差的求解，属基础题．
练习册系列答案
相关题目
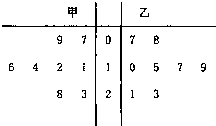（2013•内江二模）某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图：
（2013•内江二模）某篮球队甲、乙两名队员在本赛零已结束的8场比赛中得分统计的茎叶图如下：
（2012•唐山二模）某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如下：
的分布列和均值．（8分）
某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如下：