题目内容
12．关于xi（i=1，2，3，4，5）的方程x1+x2+x3+x4+x5=10（xi∈N*）的所有解的组数126（用数字作答）分析 根据题意，将原问题转化为10个小球的分组问题：假设有10个完全相同的小球，将其排成一列，利用挡板法将其分成5组，五个小组的小球数目分别对应x1、x2、x3、x4，x5，由组合数公式计算即可得答案．
解答 解：假设有10个完全相同的小球，将其排成一列，共有9个空位，
在其中选4个，插入挡板，即可将10个小球分成5组，有C94种分组方法，
第一组小球的数目是x1，第二组小球的数目是x2，第三组小球的数目是x3，第四组小球的数目是x4，第五组小球的数目是x5，
则方程的正整数解的组数就是C94=126．
故答案为：126．
点评 本题考查排列、组合的应用，关键在于将原问题进行转化，进而运用挡板法求解．
练习册系列答案
相关题目
2．已知集合A={x|x2-2x-3＜0}，B={x|y=$\sqrt{x-2}$}，则（∁RA）∪（∁RB）=（ ）
| A． | [2，3） | B． | （-∞，2）∪[3，+∞） | C． | （-∞，2）∪（3，+∞） | D． | （2，3） |
3．将一个三位数的三个数字顺序颠倒，将所得到的数与原数相加，若和中没有一个数字是偶数，则称这个数为“奇和数”．那么，所有的三位数中，奇和数有（ ）个．
| A． | 100 | B． | 120 | C． | 160 | D． | 200 |
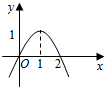已知f（x）=ax3+bx2+c，其导函数f′（x）的图象如图所示，则函数f（x）取得极小值时x的值是0．