题目内容
已知函数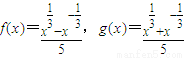 ,分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,并概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式: .
,分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,并概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式: .
【答案】分析:由已知中函数 ,代入可得f(4)-5f(2)g(2)=f(22)-5f(2)g(2)=0,f(9)-5f(3)g(3)=f(32)-5f(3)g(3)=0,分析前后各项中自变量值的关系,即可推断出一个涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式.
,代入可得f(4)-5f(2)g(2)=f(22)-5f(2)g(2)=0,f(9)-5f(3)g(3)=f(32)-5f(3)g(3)=0,分析前后各项中自变量值的关系,即可推断出一个涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式.
解答:解:由已知中函数 ,
,
∴f(4)-5f(2)g(2)
=f(22)-5f(2)g(2)
= -5•
-5• •
•
= -
-
=0
f(9)-5f(3)g(3)
=f(32)-5f(3)g(3)
= -5•
-5• •
•
= -
-
=0
由此可推断f(x2)-5f(x)g(x)=0
故答案为:f(x2)-5f(x)g(x)=0
点评:本题考查的知识点是函数的值,归纳推理,其中根据已知条件计算f(4)-5f(2)g(2)=f(22)-5f(2)g(2)=0,f(9)-5f(3)g(3)=f(32)-5f(3)g(3)=0,并分析前后各项中自变量值的关系,判断出其中的变化规律是解答本题的关键.
 ,代入可得f(4)-5f(2)g(2)=f(22)-5f(2)g(2)=0,f(9)-5f(3)g(3)=f(32)-5f(3)g(3)=0,分析前后各项中自变量值的关系,即可推断出一个涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式.
,代入可得f(4)-5f(2)g(2)=f(22)-5f(2)g(2)=0,f(9)-5f(3)g(3)=f(32)-5f(3)g(3)=0,分析前后各项中自变量值的关系,即可推断出一个涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式.解答:解:由已知中函数
 ,
,∴f(4)-5f(2)g(2)
=f(22)-5f(2)g(2)
=
 -5•
-5• •
•
=
 -
-
=0
f(9)-5f(3)g(3)
=f(32)-5f(3)g(3)
=
 -5•
-5• •
•
=
 -
-
=0
由此可推断f(x2)-5f(x)g(x)=0
故答案为:f(x2)-5f(x)g(x)=0
点评:本题考查的知识点是函数的值,归纳推理,其中根据已知条件计算f(4)-5f(2)g(2)=f(22)-5f(2)g(2)=0,f(9)-5f(3)g(3)=f(32)-5f(3)g(3)=0,并分析前后各项中自变量值的关系,判断出其中的变化规律是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
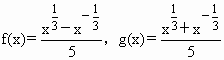 ,分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,并概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式:________.
,分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,并概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式:________.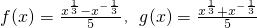 ,分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,并概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式:________.
,分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,并概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式:________.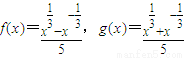 ,分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,并概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式: .
,分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,并概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式: .