题目内容
一个口袋中装有大小相同的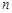 个红球(
个红球( 且
且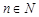 )和
)和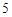 个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。
个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。
(Ⅰ)试用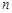 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率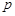 ;
;
(Ⅱ)记从口袋中三次摸奖(每次摸奖后放回)恰有一次中奖的概率为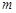 ,求
,求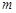 的最大值.
的最大值.
(Ⅲ)在(Ⅱ)的条件下,将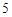 个白球全部取出后,对剩下的
个白球全部取出后,对剩下的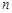 个红球全部作如下标记:记上
个红球全部作如下标记:记上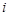 号的有
号的有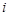 个(
个(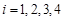 ),其余的红球记上
),其余的红球记上 号,现从袋中任取一球。
号,现从袋中任取一球。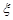 表示所取球的标号,求
表示所取球的标号,求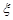 的分布列、期望和方差.
的分布列、期望和方差.
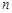 个红球(
个红球( 且
且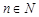 )和
)和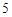 个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。
个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。(Ⅰ)试用
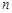 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率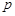 ;
;(Ⅱ)记从口袋中三次摸奖(每次摸奖后放回)恰有一次中奖的概率为
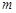 ,求
,求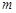 的最大值.
的最大值.(Ⅲ)在(Ⅱ)的条件下,将
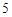 个白球全部取出后,对剩下的
个白球全部取出后,对剩下的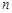 个红球全部作如下标记:记上
个红球全部作如下标记:记上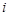 号的有
号的有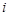 个(
个(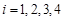 ),其余的红球记上
),其余的红球记上 号,现从袋中任取一球。
号,现从袋中任取一球。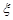 表示所取球的标号,求
表示所取球的标号,求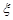 的分布列、期望和方差.
的分布列、期望和方差.(1)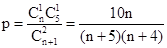 ;(2)n=20时,m的最大值为4/9;
;(2)n=20时,m的最大值为4/9;
(3)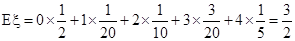 ,
,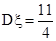 .
.
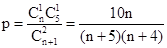 ;(2)n=20时,m的最大值为4/9;
;(2)n=20时,m的最大值为4/9;(3)
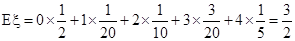 ,
,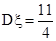 .
.第一问中,利用一次摸奖从n+5个球中任取两个,有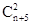 种方法。它们是等可能的,其中两个球的颜色不同的方法有
种方法。它们是等可能的,其中两个球的颜色不同的方法有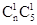 种,故一次摸奖中奖的概率为
种,故一次摸奖中奖的概率为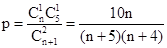 .
.
第二问中,
设每次摸奖中奖的概率为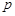 ,三次摸奖中恰有一次中奖的概率是:
,三次摸奖中恰有一次中奖的概率是:
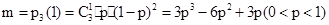 利用导数的思想求解最值。
利用导数的思想求解最值。
第三问中,由(Ⅱ)知:记上0号的有10个红球,从中任取一球,有20种取法,它们是等可能的.故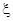 的可能取值为0,1,2,3,4求解各个概率值,然后求解期望和方差即可。
的可能取值为0,1,2,3,4求解各个概率值,然后求解期望和方差即可。
解:(Ⅰ)一次摸奖从n+5个球中任取两个,有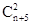 种方法。
种方法。
它们是等可能的,其中两个球的颜色不同的方法有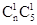 种,
种,
一次摸奖中奖的概率为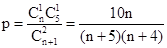 . ………5分
. ………5分
(Ⅱ)设每次摸奖中奖的概率为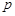 ,三次摸奖中恰有一次中奖的概率是:
,三次摸奖中恰有一次中奖的概率是:
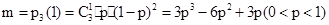 ……… 6分
……… 6分
m对p的导数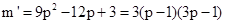
因而m在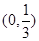 上为增函数,m在
上为增函数,m在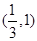 上为减函数。 ………8分
上为减函数。 ………8分
∴当p=1/3,即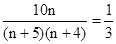 ,n=20时,m的最大值为4/9. ……… 10分
,n=20时,m的最大值为4/9. ……… 10分
(Ⅲ)由(Ⅱ)知:记上0号的有10个红球,从中任取一球,有20种取法,它们是等可能的.故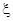 的分布列是:
的分布列是:
…12分
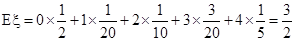 . ………14分
. ………14分
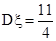 .……..15分
.……..15分
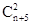 种方法。它们是等可能的,其中两个球的颜色不同的方法有
种方法。它们是等可能的,其中两个球的颜色不同的方法有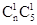 种,故一次摸奖中奖的概率为
种,故一次摸奖中奖的概率为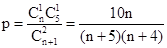 .
.第二问中,
设每次摸奖中奖的概率为
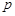 ,三次摸奖中恰有一次中奖的概率是:
,三次摸奖中恰有一次中奖的概率是: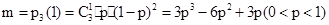 利用导数的思想求解最值。
利用导数的思想求解最值。第三问中,由(Ⅱ)知:记上0号的有10个红球,从中任取一球,有20种取法,它们是等可能的.故
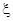 的可能取值为0,1,2,3,4求解各个概率值,然后求解期望和方差即可。
的可能取值为0,1,2,3,4求解各个概率值,然后求解期望和方差即可。解:(Ⅰ)一次摸奖从n+5个球中任取两个,有
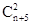 种方法。
种方法。它们是等可能的,其中两个球的颜色不同的方法有
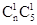 种,
种,一次摸奖中奖的概率为
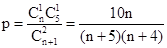 . ………5分
. ………5分(Ⅱ)设每次摸奖中奖的概率为
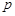 ,三次摸奖中恰有一次中奖的概率是:
,三次摸奖中恰有一次中奖的概率是: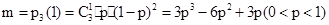 ……… 6分
……… 6分m对p的导数
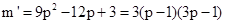
因而m在
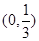 上为增函数,m在
上为增函数,m在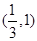 上为减函数。 ………8分
上为减函数。 ………8分∴当p=1/3,即
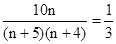 ,n=20时,m的最大值为4/9. ……… 10分
,n=20时,m的最大值为4/9. ……… 10分(Ⅲ)由(Ⅱ)知:记上0号的有10个红球,从中任取一球,有20种取法,它们是等可能的.故
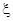 的分布列是:
的分布列是: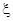 |  | 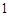 | 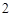 | 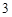 | 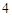 |
| p | 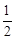 | 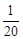 | 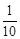 | 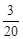 | 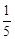 |
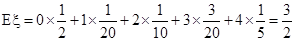 . ………14分
. ………14分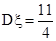 .……..15分
.……..15分
练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 ,求
,求 .
. ,则
,则 ( )
( )



 个学分;考核为优秀,授予
个学分;考核为优秀,授予 个学分.假设该校志愿者甲、乙考核为优秀的概率分别为
个学分.假设该校志愿者甲、乙考核为优秀的概率分别为 、
、 ,乙考核合格且丙考核优秀的概率为
,乙考核合格且丙考核优秀的概率为 .甲、乙、丙三人考核所得等次相互独立.
.甲、乙、丙三人考核所得等次相互独立. ,求随机变量
,求随机变量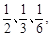 现对三只小白鼠注射这种药物.
现对三只小白鼠注射这种药物.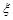 表示三只小白鼠共表现症状的种数,求
表示三只小白鼠共表现症状的种数,求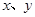 ,记
,记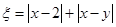 .
.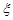 的最大值,并求事件“
的最大值,并求事件“