题目内容
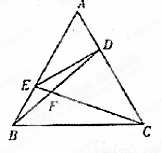
在正△ABC中，D、E分别为AB、AC的中点，则以B、C为焦点且过点D、E的双曲线的离心率为分析：首先设三角形的边长为4，并以BC为横轴，BC的中垂线为纵轴建立坐标系，进而写出A、B、C、D、E的坐标，然后根据双曲线的定义得出a的值，即可求出结果．
解答：解：以BC为横轴，BC的中垂线为纵轴，设B（-2，0）C（2，0）
则A（0，2
）D（-1，
） E（1，
），c=2，
∵椭圆与双曲线均过D，E∴2a=BE-CE=2（
-1），a=
-1，
∴e=
=
+1
故答案为
+1
则A（0，2
| 3 |
| 3 |
| 3 |
∵椭圆与双曲线均过D，E∴2a=BE-CE=2（
| 3 |
| 3 |
∴e=
| 2 | ||
|
| 3 |
故答案为
| 3 |
点评：本题考查了双曲线的定义以及性质，对于选择题与填空题可以采取灵活多样的方法作答，其中取特殊值法是常用方法．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
在正△ABC中，D∈AB，E∈AC，向量
=
，则以B，C为焦点，且过D，E的双曲线离心率为（ ）
| DE |
| 1 |
| 2 |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
AC,AE=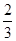
AB,BD,CE相交于点F.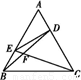
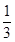AC,AE=
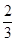AB,BD,CE相交于点F.