题目内容
14．如图，在△ABC中，∠C=90°，AD为∠BAC的角平分线，BC=64，BD：DC=9：7．求点D到AB的距离．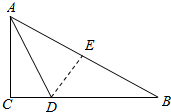
分析 过D作DE⊥AB于E，根据角平分线的性质可以得到DE=CD，而根据已知条件可以求出CD的长，也就求出了DE的长．
解答 解：如图，过D作DE⊥AB于E，
∵AD平分∠BAC交BC于D，而∠C=90°，
∴CD=DE，
∵BC=64，且BD：CD=9：7，
∴CD=64×$\frac{7}{9+7}$=28，
∴DE=28，则点D到AB边的距离为28．
点评 此题主要利用角平分线的性质解题，把求则点D到AB的距离转化成求CD的长．
练习册系列答案
教材全解字词句篇系列答案
相关题目
5．直线$\frac{x}{a}$-$\frac{y}{b}$=1与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的公共点个数为（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 不确定 |
19．在数列{an}中，对任意正整数n都有an+1-2an=0（an≠0），则$\frac{2{a}_{1}+{a}_{2}}{2{a}_{3}+{a}_{4}}$=（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | 1 |