题目内容
已知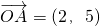 ,
,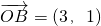 ,
,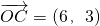 ,在
,在 上是否存在点M,使
上是否存在点M,使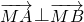 ,若存在,求出点M的坐标;若不存在,请说明理由.
,若存在,求出点M的坐标;若不存在,请说明理由.
解:设存在点M,且 (0<λ≤1),
(0<λ≤1),
∴ ,
,
 .
.
∵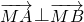 ,
,
∴(2-6λ)(3-6λ)+(5-3λ)(1-3λ)=0,
即45λ2-48λ+11=0,
解得 .
.
∴ =(2,1)或
=(2,1)或 =(
=( ,
,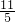 ).
).
∴存在M(2,1)或M( ,
,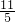 )满足题意.
)满足题意.
分析:利用三点共线即向量共线,利用向量共线的充要条件表示出M的坐标;利用向量的坐标公式求出向量的坐标;利用向量垂直的充要条件列出方程,求出M的坐标.
点评:本题考查向量共线的充要条件、考查向量垂直的充要条件:数量积为0、考查向量的数量积公式.
 (0<λ≤1),
(0<λ≤1),∴
 ,
, .
.∵
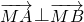 ,
,∴(2-6λ)(3-6λ)+(5-3λ)(1-3λ)=0,
即45λ2-48λ+11=0,
解得
 .
.∴
 =(2,1)或
=(2,1)或 =(
=( ,
,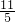 ).
).∴存在M(2,1)或M(
 ,
,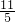 )满足题意.
)满足题意.分析:利用三点共线即向量共线,利用向量共线的充要条件表示出M的坐标;利用向量的坐标公式求出向量的坐标;利用向量垂直的充要条件列出方程,求出M的坐标.
点评:本题考查向量共线的充要条件、考查向量垂直的充要条件:数量积为0、考查向量的数量积公式.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 是定义在
是定义在 上的奇函数,并且在
上的奇函数,并且在 上是减函数.是否存
上是减函数.是否存 使
使 恒成立?若存在,求出实数
恒成立?若存在,求出实数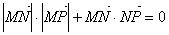
 与曲线C交于A、B两点,那么在曲线C上是否存
与曲线C交于A、B两点,那么在曲线C上是否存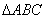 是以AB为斜边的直角三角形?若存在,求出m的取值范围;若不存在,
是以AB为斜边的直角三角形?若存在,求出m的取值范围;若不存在,