题目内容
不等式x+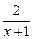
>2的解集是
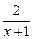>2的解集是| A．(－1,0)∪(1,+∞) | B．(－∞,－1)∪(0,1) |
| C．(－1,0)∪(0,1) | D．(－∞,－1)∪(1,+∞) |
A
解法一:通过移项、整理,原不等式可变为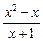
>0,
即
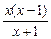>0.
利用“穿线法”解此不等式,如下图.
得不等式的解集为{x|－1<x<0或x>1}.
解法二:利用数形结合法.
原不等式可化为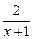>2－x,
构造两个函数f(x)=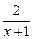,g(x)=2－x,看当x取什么范围时,f(x)的图象在g(x)的上方.如下图所示.
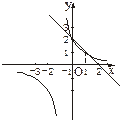
不等式的解集为{x|－1<x<0或x>1}.
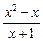>0,即
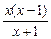>0.利用“穿线法”解此不等式,如下图.
得不等式的解集为{x|－1<x<0或x>1}.
解法二:利用数形结合法.
原不等式可化为
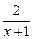>2－x,构造两个函数f(x)=
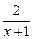,g(x)=2－x,看当x取什么范围时,f(x)的图象在g(x)的上方.如下图所示.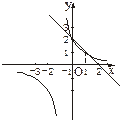不等式的解集为{x|－1<x<0或x>1}.
练习册系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
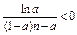对于任意正整数n恒成立， 则实数a的取值范围是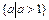
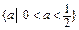
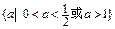
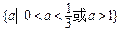
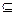［1，4］，求实数a的取值范围？
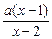＞1(a≠1)。
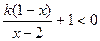(k≥0，k≠1).
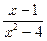>0的解集为
＋
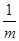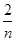的最小值等于________．
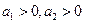且
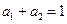时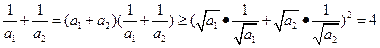
。类比上述方法可得：当
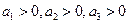且
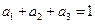时，有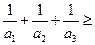
；你能否把上述结论作一些正确的推广： 。
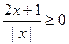的解集为 。