题目内容
已知可行域 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率 .
.
(1)求圆C及椭圆C1的方程;
(2)设椭圆C1的右焦点为F,点P为圆C上异于A1、A2的动点,过原点O作直线PF的垂线交直线 于点Q,判断直线PQ与圆C的位置关系,并给出证明.
于点Q,判断直线PQ与圆C的位置关系,并给出证明.
 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率 .
.(1)求圆C及椭圆C1的方程;
(2)设椭圆C1的右焦点为F,点P为圆C上异于A1、A2的动点,过原点O作直线PF的垂线交直线
 于点Q,判断直线PQ与圆C的位置关系,并给出证明.
于点Q,判断直线PQ与圆C的位置关系,并给出证明.解:(1):解方程组 ,得:y=0,x=﹣2,
,得:y=0,x=﹣2,
 ,得:y=0,x=2,
,得:y=0,x=2,
 ,得:y=
,得:y= ,x=1,
,x=1,
∴可行域y的三个顶点分别为:(﹣2,0),(2,0),(1, ),
),
设圆的方程为:x2+y2+Dx+Ey+F=0,得到方程组: ,
,
解得:D=0,E=0,F=﹣4,
∴圆C的方程为:x2+y2=4,
圆与X轴的交点A1(﹣2,0),A2(2,0),
设椭圆C1的方程的方程为: ,(a>b>0)
,(a>b>0)
则有 ,
,
∴椭圆方程为:
(2)设p(x0,y0),(x0≠±2),
∴当x0= 时,P(2,
时,P(2, ),
), ,kOp·kPQ=﹣1,
,kOp·kPQ=﹣1,
当 时,
时, ,
, ,
,
∴ ,
,
∴ ,
,
∴KOP·KPQ=﹣1,故相切.
 ,得:y=0,x=﹣2,
,得:y=0,x=﹣2, ,得:y=0,x=2,
,得:y=0,x=2, ,得:y=
,得:y= ,x=1,
,x=1,∴可行域y的三个顶点分别为:(﹣2,0),(2,0),(1,
 ),
),设圆的方程为:x2+y2+Dx+Ey+F=0,得到方程组:
 ,
,解得:D=0,E=0,F=﹣4,
∴圆C的方程为:x2+y2=4,
圆与X轴的交点A1(﹣2,0),A2(2,0),
设椭圆C1的方程的方程为:
 ,(a>b>0)
,(a>b>0)则有
 ,
,∴椭圆方程为:

(2)设p(x0,y0),(x0≠±2),
∴当x0=
 时,P(2,
时,P(2, ),
), ,kOp·kPQ=﹣1,
,kOp·kPQ=﹣1,当
 时,
时, ,
, ,
,∴
 ,
, ∴
 ,
, ∴KOP·KPQ=﹣1,故相切.

练习册系列答案
相关题目
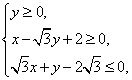 的外接圆C与
的外接圆C与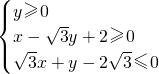 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率 .
. 于点Q,判断直线PQ与圆C的位置关系,并给出证明.
于点Q,判断直线PQ与圆C的位置关系,并给出证明. 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率 .
. 于点Q,判断直线PQ与圆C的位置关系,并给出证明.
于点Q,判断直线PQ与圆C的位置关系,并给出证明. 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率 .
. 于点Q,判断直线PQ与圆C的位置关系,并给出证明.
于点Q,判断直线PQ与圆C的位置关系,并给出证明.