题目内容
研究某灌溉渠道水的流速y与水深x之间的关系,测得一组数据如下:水深x/m | 1.40 | 1.50 | 1.60 | 1.70 | 1.80 | 1.90 | 2.00 | 2.10 |
流速y/(m·s-1) | 1.70 | 1.79 | 1.88 | 1.95 | 2.03 | 2.10 | 2.16 | 2.21 |
(1)求y对x的回归直线方程;
(2)预测水深为1.95 m时水的流速是多少?
解析:(1)这8对数据描绘在平面直角坐标系中,得到平面上8个点,如图所示.
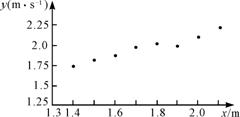
由图容易看出,x与y之间有近似的线性相关关系,或者说,可以设回归直线方程=a+bx.
可采用列表的方法计算a与回归系数b,
序号 | x | y | x2 | x |
y | 1 | 1.40 | 1.70 | 1.96 |
2.380 | 2 | 1.50 | 1.79 | 2.25 |
2.685 | 3 | 1.60 | 1.88 | 2.56 |
3.008 | 4 | 1.70 | 1.95 | 2.89 |
3.315 | 5 | 1.80 | 2.03 | 3.24 |
3.654 | 6 | 1.90 | 2.10 | 3.61 |
3.990 | 7 | 2.00 | 2.16 | 4.00 |
4.320 | 8 | 2.10 | 2.21 | 4.41 |
4.641 | ∑ | 14.00 | 15.82 | 24.92 |
于是,![]() =
=![]() ×14.00=1.75,
×14.00=1.75,![]() =
=![]() ×15.82=1.977 5,
×15.82=1.977 5,
![]() ≈0.733.
≈0.733.
![]() =1.977 5-
=1.977 5-![]() ×1.75≈0.694.y对x的回归直线方程为
×1.75≈0.694.y对x的回归直线方程为![]() =0.694+0.733x.
=0.694+0.733x.
回归系数=0.733的意思是,在此灌溉渠道中,水深每增加0.1 m,水的流速平均增加0.073 3 m/s(本例数据是以0.1 m为水深间隔测得的),![]() =0.694可以解释为水的流速中不受水深影响的部分.
=0.694可以解释为水的流速中不受水深影响的部分.
(2)由(1)中求出的回归直线方程,把x=1.95代入,易得
![]() =0.694+0.733×1.95≈2.12(m/s).
=0.694+0.733×1.95≈2.12(m/s).
计算结果表明,当水深为1.95 m时可以预测水的流速约为2.12 m/s.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| ? |
| y |
| A、0.733m/s |
| B、0.0733m/s |
| C、0.6942m/s |
| D、0.06942m/s |
水深x/m | 1.40 | 1.50 | 1.60 | 1.70 | 1.80 | 1.90 | 2.00 | 2.10 |
流速Y/(m·s-1) | 1.70 | 1.79 | 1.88 | 1.95 | 2.03 | 2.10 | 2.16 | 2.21 |
(1)求Y对x的回归直线方程;
(2)预测水深为
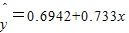 ,那么在此灌溉渠道中,水深每增加0.1m,水的流速平均增加( )
,那么在此灌溉渠道中,水深每增加0.1m,水的流速平均增加( )