题目内容
在△ABC中,已知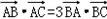 。
。
(1)求证:tanB=3tanA;
(2)若cosC=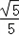 ,求A的值。
,求A的值。
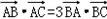 。
。(1)求证:tanB=3tanA;
(2)若cosC=
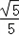 ,求A的值。
,求A的值。解:(1)∵ ·
· =3
=3 ·
· ,
,
∴cbcosA=3cacosB,
即bcosA=3acosB,
由正弦定理 =
= 得:sinBcosA=3sinAcosB,
得:sinBcosA=3sinAcosB,
又0<A+B<π,
∴cosA>0,cosB>0,
在等式两边同时除以cosAcosB,可
得tanB=3tanA;
(2)∵cosC= ,0<C<π,
,0<C<π,
sinC= =
= ,
,
∴tanC=2,
tan[π-(A+B)]=2,即tan(A+B)=-2,
∴ =-2,将tanB=3tanA代入得:
=-2,将tanB=3tanA代入得: =-2,
=-2,
整理得:3tan2A-2tanA-1=0,
即(tanA-1)(3tanA+1)=0,
解得:tanA=1或tanA=- ,
,
又coaA>0,
∴tanA=1,
又A为三角形的内角,则A= 。
。
 ·
· =3
=3 ·
· ,
,∴cbcosA=3cacosB,
即bcosA=3acosB,
由正弦定理
 =
= 得:sinBcosA=3sinAcosB,
得:sinBcosA=3sinAcosB,又0<A+B<π,
∴cosA>0,cosB>0,
在等式两边同时除以cosAcosB,可
得tanB=3tanA;
(2)∵cosC=
 ,0<C<π,
,0<C<π,sinC=
 =
= ,
,∴tanC=2,
tan[π-(A+B)]=2,即tan(A+B)=-2,
∴
 =-2,将tanB=3tanA代入得:
=-2,将tanB=3tanA代入得: =-2,
=-2,整理得:3tan2A-2tanA-1=0,
即(tanA-1)(3tanA+1)=0,
解得:tanA=1或tanA=-
 ,
,又coaA>0,
∴tanA=1,
又A为三角形的内角,则A=
 。
。
练习册系列答案
相关题目