题目内容
已知椭圆的两个焦点F1(0,1)、F2(0,1)、直线y=4是它的一条准线,A1、A2分别是椭圆的上、下两个顶点.(Ⅰ)求椭圆的方程;
(Ⅱ)设以原点为顶点,A1点的抛物线为C,若过点F1的直线l与C交于不同的两点M、N,求线段MN的中点Q的轨迹方程.
【答案】分析:(Ⅰ)设椭圆方程为 ,由题意,得
,由题意,得 ,由此能求出椭圆方程.
,由此能求出椭圆方程.
(Ⅱ)设抛物线C的方程为x2=2py,p>0.由 ,得p=4.故抛物线C的方程为x2=8y,设线段MN的中点Q(x,y),直线l的方程为y=kx+1,由
,得p=4.故抛物线C的方程为x2=8y,设线段MN的中点Q(x,y),直线l的方程为y=kx+1,由 ,得x2-8kx-8=0,设M(x1,y1),N(x2,y2),则x1+x2=8k,x1x2=-8.故
,得x2-8kx-8=0,设M(x1,y1),N(x2,y2),则x1+x2=8k,x1x2=-8.故 ,代入直线l的方程,得y=k•4k+1=4k2+1,由此能求出点Q的轨迹方程.
,代入直线l的方程,得y=k•4k+1=4k2+1,由此能求出点Q的轨迹方程.
解答:解:(Ⅰ)设椭圆方程为 ,
,
由题意,得 ,
,
∴a2=4,b2=4-1=3,
∴所求椭圆方程 ; …(5分)
; …(5分)
(Ⅱ)设抛物线C的方程为x2=2py,p>0.
由 ,得p=4.
,得p=4.
∴抛物线C的方程为x2=8y,
设线段MN的中点Q(x,y),直线l的方程为y=kx+1,
由 ,得x2=8kx+8,
,得x2=8kx+8,
即x2-8kx-8=0,设M(x1,y1),N(x2,y2),
则有x1+x2=8k,x1x2=-8.
∴ ,
,
代入直线l的方程,得y=k•4k+1=4k2+1,
由 ,消去k,得
,消去k,得 ,
,
即x2=4(y-1),
∴点Q的轨迹方程是x2=4(y-1).
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,抛物线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
 ,由题意,得
,由题意,得 ,由此能求出椭圆方程.
,由此能求出椭圆方程.(Ⅱ)设抛物线C的方程为x2=2py,p>0.由
 ,得p=4.故抛物线C的方程为x2=8y,设线段MN的中点Q(x,y),直线l的方程为y=kx+1,由
,得p=4.故抛物线C的方程为x2=8y,设线段MN的中点Q(x,y),直线l的方程为y=kx+1,由 ,得x2-8kx-8=0,设M(x1,y1),N(x2,y2),则x1+x2=8k,x1x2=-8.故
,得x2-8kx-8=0,设M(x1,y1),N(x2,y2),则x1+x2=8k,x1x2=-8.故 ,代入直线l的方程,得y=k•4k+1=4k2+1,由此能求出点Q的轨迹方程.
,代入直线l的方程,得y=k•4k+1=4k2+1,由此能求出点Q的轨迹方程.解答:解:(Ⅰ)设椭圆方程为
 ,
,由题意,得
 ,
,∴a2=4,b2=4-1=3,
∴所求椭圆方程
 ; …(5分)
; …(5分)(Ⅱ)设抛物线C的方程为x2=2py,p>0.
由
 ,得p=4.
,得p=4.∴抛物线C的方程为x2=8y,
设线段MN的中点Q(x,y),直线l的方程为y=kx+1,
由
 ,得x2=8kx+8,
,得x2=8kx+8,即x2-8kx-8=0,设M(x1,y1),N(x2,y2),
则有x1+x2=8k,x1x2=-8.
∴
 ,
,代入直线l的方程,得y=k•4k+1=4k2+1,
由
 ,消去k,得
,消去k,得 ,
,即x2=4(y-1),
∴点Q的轨迹方程是x2=4(y-1).
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,抛物线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
相关题目
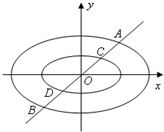 定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆 的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B.
的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B. ,求直线l的方程;
,求直线l的方程; ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围.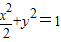 的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B.
的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B. ,求直线l的方程;
,求直线l的方程; ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围. .
. ,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由;
,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由; 和
和 分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
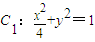 .
. ,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由;
,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由; 和
和 分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)