Question

【题目】双曲线的虚轴长为，两条渐近线方程为.

（1）求双曲线的方程；

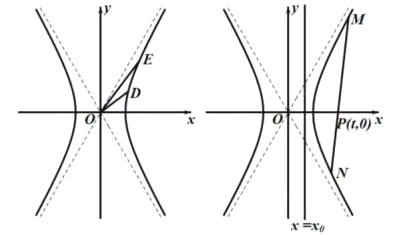
（2）双曲线上有两个点，直线和的斜率之积为，判别是否为定值，；

（3）经过点的直线且与双曲线有两个交点，直线的倾斜角是，是否存在直线（其中）使得恒成立？（其中分别是点到的距离）若存在，求出的值，若不存在，请说明理由.

Answer 1

【答案】（1）；（2）8；（3）存在且

【解析】分析：（1）根据题意，双曲线的虚轴长为，两条渐近线方程为.易求求双曲线的方程；

（2）设直线的斜率，显然，

联立得，求出，，可证；

（3）设直线方程，

联立，（*），

∵，方程总有两个解，

设，得到，

根据得，整理得，由，则符合题目要求，存在直线．

详解：

（1）双曲线；

（2）设直线的斜率，显然，

联立得，

，

，

；

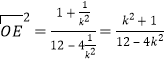（3）设直线方程，

联立，（*），

∵，方程总有两个解，

设，

，

根据得，

整理得，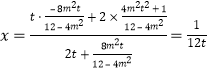

∵，

∴符合题目要求，存在直线．