Question

四面体ABCD中，E是AD中点，F是BC中点，AB=DC=1，EF=

1

2

，则直线AB与DC所成的角大小为

 

．

Answer 1

分析：取AC中点M，连接MF、ME，因为MF∥AB，ME∥CD，所以异面直线AB与DC所成的角即为直线MF与ME所成的角，即∠FME．

解答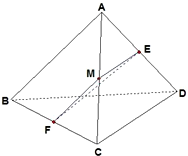：解：如图所示：
取AC中点M，连接MF、ME
∵在四面体ABCD中，E是AD中点，F是BC中点，
∴MF=

1

2

AB=

1

2

，ME=

1

2

DC=

1

2

又∵EF=

1

2

∴△MFE为等边三角形
∴∠FME=60°
又∵MF∥AB，ME∥CD
∴异面直线AB与DC所成的角即为直线MF与ME所成的角，即∠FME
∴直线AB与DC所成的角的大小为

π

3

．
故答案为：

π

3

点评：本题主要考查了异面直线所成的角，空间中的线面关系，解三角形等基础知识，考查空间想象能力和思维能力．