题目内容
已知向量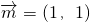 ,向量
,向量 与向量
与向量 夹角为
夹角为 ,且
,且 .
.
(1)若向量 与向量
与向量 =(1,0)的夹角为
=(1,0)的夹角为 ,向量
,向量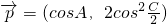 ,其中A,C为△ABC的内角,且A,B,C依次成等差数列,试求|
,其中A,C为△ABC的内角,且A,B,C依次成等差数列,试求| +
+ |的取值范围.
|的取值范围.
(2)若A、B、C为△ABC的内角,且A,B,C依次成等差数列,A≤B≤C,设f(A)=sin2A-2(sinA+cosA)+a2,f(A)的最大值为 ,关于x的方程
,关于x的方程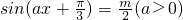 在
在 上有相异实根,求m的取值范围.
上有相异实根,求m的取值范围.
解:(1)令 =(x,y),则有cos
=(x,y),则有cos =
= =-
=-
由 得
得 ,又向量
,又向量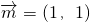 ,故其模为
,故其模为 ,
,
则向量 人模为1.则有x2+y2=1
人模为1.则有x2+y2=1
(1)向量 与向量
与向量 =(1,0)的夹角为
=(1,0)的夹角为 ,故有
,故有 •
• =0,即x=0,故y=±1
=0,即x=0,故y=±1
又 故y=-1,则
故y=-1,则 =(0,-1),
=(0,-1),
向量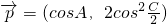 ,即
,即
又A,C为△ABC的内角,且A,B,C依次成等差数列 故B=
| +
+ |2=cos2A+cos2C=cos2A+cos2(
|2=cos2A+cos2C=cos2A+cos2( -A)=1+
-A)=1+ cos(2A+
cos(2A+ )
)
由A∈(0, ),得2A+
),得2A+ ∈(
∈( ,
, )得cos(2A+
)得cos(2A+ )∈[-1,
)∈[-1, )
)
| +
+ |2∈[
|2∈[ ,
, )故|
)故| +
+ |∈[
|∈[ ,
, )
)
(2∵A、B、C为△ABC的内角,且A,B,C依次成等差数列,A≤B≤C,∴B=
∴f(A)=sin2A-2(sinA+cosA)+a2=2sinAcosA-2(sinA+cosA)+a2
令t=sinA+cosA= sin(A+
sin(A+ ),则2sinAcosA=t2-1
),则2sinAcosA=t2-1
由于A∈(0, ],A+
],A+ ∈(
∈( ,
, ],故t=
],故t= sin(A+
sin(A+ )∈(1,
)∈(1, ]
]
故有f(A)=t2-1-2t+a2=t2-2t+a2-1,t∈(1, ]
]
当t= 时取到最大值为1-2
时取到最大值为1-2 +a2
+a2
又f(A)的最大值为 ,故1-2
,故1-2 +a2=
+a2=
故a2=4,又a>0,故a=2
又关于的方程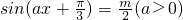 在
在 上有相异实根
上有相异实根
即方程 在
在 上有相异实根
上有相异实根
因为x∈ ,故y=
,故y= 在(0,
在(0, )上是增函数,在(
)上是增函数,在( ,
, )上是减函数
)上是减函数
方程 在
在 上有相异实根
上有相异实根
故 ∈[
∈[ ,1),
,1),
故m∈[ ,2).
,2).
分析:由题意先求出向量 的坐标满足有x2+y2=1
的坐标满足有x2+y2=1
(1)由向量 与向量
与向量 =(1,0)的夹角为
=(1,0)的夹角为 ,故有
,故有 •
• =0,由此解出向量
=0,由此解出向量 的坐标,代入|
的坐标,代入| +
+ |2,用相关公式求其范围,进而求出|
|2,用相关公式求其范围,进而求出| +
+ |∈[
|∈[ ,
, )
)
(2)先解出B= ,确定出A的范围,再对f(A)用换元法变形,求出其最值的表达式,判断并求出其最大值是1-2
,确定出A的范围,再对f(A)用换元法变形,求出其最值的表达式,判断并求出其最大值是1-2 +a2,又已知f(A)的最大值为
+a2,又已知f(A)的最大值为 ,令两者相等解出参数a的值,再由
,令两者相等解出参数a的值,再由 在
在 上有相异实根,依据三角函数的性质求出参数m满足的范围.
上有相异实根,依据三角函数的性质求出参数m满足的范围.
点评:本题考点是三角函数的最值,综合利用二次函数的最值,向量的运算,三角函数的恒等变形,三角函数的最值,及三角函数的图象,涉及到知识广度高,综合性强,做题时要有耐心地对题目中所给的每一个条件细心、严谨转化,对每一个条件所蕴含的本质进行挖掘,逐步向结论靠近,如本题中第二小题,逐层推进比较明显,答题过程中仔细体会此思维脉络.
 =(x,y),则有cos
=(x,y),则有cos =
= =-
=-
由
 得
得 ,又向量
,又向量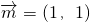 ,故其模为
,故其模为 ,
,则向量
 人模为1.则有x2+y2=1
人模为1.则有x2+y2=1(1)向量
 与向量
与向量 =(1,0)的夹角为
=(1,0)的夹角为 ,故有
,故有 •
• =0,即x=0,故y=±1
=0,即x=0,故y=±1又
 故y=-1,则
故y=-1,则 =(0,-1),
=(0,-1),向量
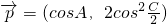 ,即
,即
又A,C为△ABC的内角,且A,B,C依次成等差数列 故B=

|
 +
+ |2=cos2A+cos2C=cos2A+cos2(
|2=cos2A+cos2C=cos2A+cos2( -A)=1+
-A)=1+ cos(2A+
cos(2A+ )
)由A∈(0,
 ),得2A+
),得2A+ ∈(
∈( ,
, )得cos(2A+
)得cos(2A+ )∈[-1,
)∈[-1, )
)|
 +
+ |2∈[
|2∈[ ,
, )故|
)故| +
+ |∈[
|∈[ ,
, )
)(2∵A、B、C为△ABC的内角,且A,B,C依次成等差数列,A≤B≤C,∴B=

∴f(A)=sin2A-2(sinA+cosA)+a2=2sinAcosA-2(sinA+cosA)+a2
令t=sinA+cosA=
 sin(A+
sin(A+ ),则2sinAcosA=t2-1
),则2sinAcosA=t2-1由于A∈(0,
 ],A+
],A+ ∈(
∈( ,
, ],故t=
],故t= sin(A+
sin(A+ )∈(1,
)∈(1, ]
]故有f(A)=t2-1-2t+a2=t2-2t+a2-1,t∈(1,
 ]
]当t=
 时取到最大值为1-2
时取到最大值为1-2 +a2
+a2又f(A)的最大值为
 ,故1-2
,故1-2 +a2=
+a2=
故a2=4,又a>0,故a=2
又关于的方程
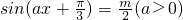 在
在 上有相异实根
上有相异实根即方程
 在
在 上有相异实根
上有相异实根因为x∈
 ,故y=
,故y= 在(0,
在(0, )上是增函数,在(
)上是增函数,在( ,
, )上是减函数
)上是减函数方程
 在
在 上有相异实根
上有相异实根故
 ∈[
∈[ ,1),
,1),故m∈[
 ,2).
,2).分析:由题意先求出向量
 的坐标满足有x2+y2=1
的坐标满足有x2+y2=1(1)由向量
 与向量
与向量 =(1,0)的夹角为
=(1,0)的夹角为 ,故有
,故有 •
• =0,由此解出向量
=0,由此解出向量 的坐标,代入|
的坐标,代入| +
+ |2,用相关公式求其范围,进而求出|
|2,用相关公式求其范围,进而求出| +
+ |∈[
|∈[ ,
, )
)(2)先解出B=
 ,确定出A的范围,再对f(A)用换元法变形,求出其最值的表达式,判断并求出其最大值是1-2
,确定出A的范围,再对f(A)用换元法变形,求出其最值的表达式,判断并求出其最大值是1-2 +a2,又已知f(A)的最大值为
+a2,又已知f(A)的最大值为 ,令两者相等解出参数a的值,再由
,令两者相等解出参数a的值,再由 在
在 上有相异实根,依据三角函数的性质求出参数m满足的范围.
上有相异实根,依据三角函数的性质求出参数m满足的范围.点评:本题考点是三角函数的最值,综合利用二次函数的最值,向量的运算,三角函数的恒等变形,三角函数的最值,及三角函数的图象,涉及到知识广度高,综合性强,做题时要有耐心地对题目中所给的每一个条件细心、严谨转化,对每一个条件所蕴含的本质进行挖掘,逐步向结论靠近,如本题中第二小题,逐层推进比较明显,答题过程中仔细体会此思维脉络.

练习册系列答案
相关题目
 ,向量
,向量 与向量
与向量 夹角为
夹角为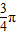 ,且
,且 ,又A、B、C为△ABC的三个内角,且B=
,又A、B、C为△ABC的三个内角,且B= ,A≤B≤C.
,A≤B≤C. ;
; 与向量
与向量 的夹角为
的夹角为 ,向量
,向量 ,试求
,试求 的取值范围.
的取值范围. =
= ,向量
,向量 与向量
与向量 关于x轴对称.
关于x轴对称. 的解析式,并求其单调增区间;
的解析式,并求其单调增区间; =
= ,向量
,向量 与向量
与向量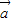 关于x轴对称.
关于x轴对称. 的解析式,并求其单调增区间;
的解析式,并求其单调增区间; =
= ,向量
,向量 与向量
与向量 关于x轴对称.
关于x轴对称. 的解析式,并求其单调增区间;
的解析式,并求其单调增区间; ,向量
,向量 与向量
与向量 的夹角为
的夹角为 ,且
,且 ;
; ,向量
,向量 ,其中
,其中 ,若
,若 ,求
,求 的取值范围
的取值范围