题目内容
已知向量 ,向量
,向量 与向量
与向量 夹角为
夹角为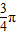 ,且
,且 ,又A、B、C为△ABC的三个内角,且B=
,又A、B、C为△ABC的三个内角,且B= ,A≤B≤C.
,A≤B≤C.(Ⅰ)求向量
 ;
;(Ⅱ)若向量
 与向量
与向量 的夹角为
的夹角为 ,向量
,向量 ,试求
,试求 的取值范围.
的取值范围.
【答案】分析:(Ⅰ)设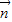 =(x,y),由
=(x,y),由 可得x+y=-1,由向量
可得x+y=-1,由向量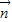 与向量
与向量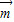 夹角为
夹角为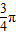 ,求得x2+y2=1,解方程组求得x、y的值,即可求得向量
,求得x2+y2=1,解方程组求得x、y的值,即可求得向量 的坐标.
的坐标.
(Ⅱ)由向量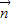 与向量
与向量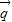 =(1,0)垂直知
=(1,0)垂直知 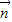 =(0,-1),求得
=(0,-1),求得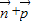 的坐标,可求得
的坐标,可求得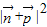 的解析式为
的解析式为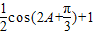 ,再根据余弦函数的定义域和值域,求得
,再根据余弦函数的定义域和值域,求得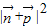 的范围,即可得到
的范围,即可得到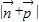 的取值范围.
的取值范围.
解答:解:(Ⅰ)设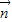 =(x,y),由
=(x,y),由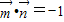 可得x+y=-1. ①…(2分)
可得x+y=-1. ①…(2分)
由向量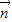 与向量
与向量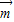 夹角为
夹角为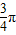 ,得
,得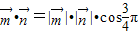 ,∴
,∴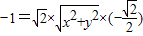 ,得x2+y2=1.②…(4分)
,得x2+y2=1.②…(4分)
由①②解得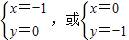 ,可得
,可得 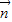 =(-1,0),或
=(-1,0),或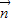 =(0,-1). …(6分)
=(0,-1). …(6分)
(Ⅱ)由向量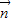 与向量
与向量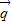 =(1,0)垂直知
=(1,0)垂直知 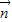 =(0,-1). …(7分)
=(0,-1). …(7分)
∵△ABC的三个内角中,B=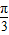 ,A≤B≤C,∴
,A≤B≤C,∴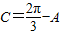 ,
,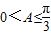 . …(8分)
. …(8分)
∴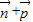 =(cosA,
=(cosA, -1)=(cosA,cosC),…(9分)
-1)=(cosA,cosC),…(9分)
∴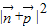 =cos2A+cos2C=
=cos2A+cos2C= …(10分)
…(10分)
=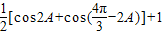 =
=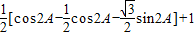 =
=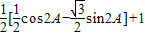 =
=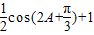 . …(12分)
. …(12分)
∵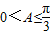 ,∴
,∴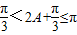 ,∴
,∴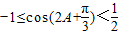 ,∴
,∴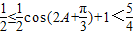 .
.
∴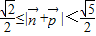 ,即
,即 的取值范围是
的取值范围是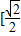 ,
,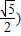 . …(14分)
. …(14分)
点评:本题主要考查两个向量的数量积公式、求向量的模 的方法,三角恒等变换,余弦函数的定义域和值域,属于中档题.
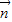 =(x,y),由
=(x,y),由 可得x+y=-1,由向量
可得x+y=-1,由向量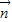 与向量
与向量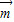 夹角为
夹角为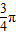 ,求得x2+y2=1,解方程组求得x、y的值,即可求得向量
,求得x2+y2=1,解方程组求得x、y的值,即可求得向量 的坐标.
的坐标.(Ⅱ)由向量
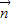 与向量
与向量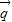 =(1,0)垂直知
=(1,0)垂直知 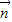 =(0,-1),求得
=(0,-1),求得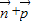 的坐标,可求得
的坐标,可求得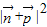 的解析式为
的解析式为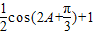 ,再根据余弦函数的定义域和值域,求得
,再根据余弦函数的定义域和值域,求得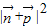 的范围,即可得到
的范围,即可得到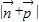 的取值范围.
的取值范围.解答:解:(Ⅰ)设
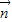 =(x,y),由
=(x,y),由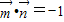 可得x+y=-1. ①…(2分)
可得x+y=-1. ①…(2分)由向量
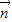 与向量
与向量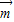 夹角为
夹角为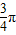 ,得
,得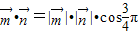 ,∴
,∴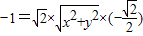 ,得x2+y2=1.②…(4分)
,得x2+y2=1.②…(4分)由①②解得
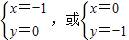 ,可得
,可得 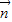 =(-1,0),或
=(-1,0),或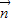 =(0,-1). …(6分)
=(0,-1). …(6分)(Ⅱ)由向量
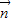 与向量
与向量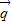 =(1,0)垂直知
=(1,0)垂直知 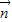 =(0,-1). …(7分)
=(0,-1). …(7分)∵△ABC的三个内角中,B=
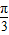 ,A≤B≤C,∴
,A≤B≤C,∴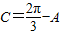 ,
,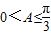 . …(8分)
. …(8分)∴
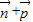 =(cosA,
=(cosA, -1)=(cosA,cosC),…(9分)
-1)=(cosA,cosC),…(9分)∴
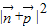 =cos2A+cos2C=
=cos2A+cos2C= …(10分)
…(10分)=
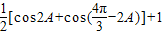 =
=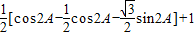 =
=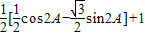 =
=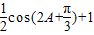 . …(12分)
. …(12分)∵
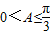 ,∴
,∴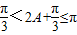 ,∴
,∴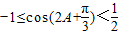 ,∴
,∴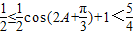 .
.∴
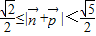 ,即
,即 的取值范围是
的取值范围是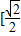 ,
,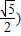 . …(14分)
. …(14分)点评:本题主要考查两个向量的数量积公式、求向量的模 的方法,三角恒等变换,余弦函数的定义域和值域,属于中档题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 =
= ,向量
,向量 与向量
与向量 关于x轴对称.
关于x轴对称. 的解析式,并求其单调增区间;
的解析式,并求其单调增区间; =
= ,向量
,向量 与向量
与向量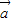 关于x轴对称.
关于x轴对称. 的解析式,并求其单调增区间;
的解析式,并求其单调增区间; =
= ,向量
,向量 与向量
与向量 关于x轴对称.
关于x轴对称. 的解析式,并求其单调增区间;
的解析式,并求其单调增区间; ,向量
,向量 与向量
与向量 的夹角为
的夹角为 ,且
,且 ;
; ,向量
,向量 ,其中
,其中 ,若
,若 ,求
,求 的取值范围
的取值范围