Question

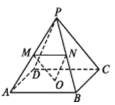
【题目】如图,在棱长均相等的四棱锥中, 为底面正方形的中心, ,分别为侧棱,的中点,有下列结论正确的有：( )

A.∥平面B.平面∥平面

C.直线与直线所成角的大小为D.

Answer 1

【答案】ABD

【解析】

选项A,利用线面平行的判定定理即可证明；选项B,先利用线面平行的判定定理证明CD∥平面OMN，再利用面面平行的判定定理即可证明；选项C，平移直线，找到线面角，再计算；选项D,因为ON∥PD，所以只需证明PD⊥PB，利用勾股定理证明即可.

选项A,连接BD，显然O为BD的中点，又N为PB的中点，所以∥ON,由线面平行的判定定理可得，∥平面；选项B, 由,分别为侧棱,的中点,得MN∥AB,又底面为正方形，所以MN∥CD，由线面平行的判定定理可得，CD∥平面OMN,又选项A得∥平面，由面面平行的判定定理可得，平面∥平面；选项C,因为MN∥CD，所以∠ PDC为直线与直线所成的角，又因为所有棱长都相等，所以∠ PDC=，故直线与直线所成角的大小为；选项D，因底面为正方形，所以,又所有棱长都相等，所以,故,又

∥ON，所以，故ABD均正确.