题目内容
7.设函数f(x)=2x3+3ax2+3bx+8c在x=1及x=2时取得极值.(1)求a、b的值;
(2)若对于任意的x∈[0,3],都有f(x)<c2成立,求c的取值范围.
分析 (1)根据已知条件可得关于a,b的方程组,解出并验证即可;
(2)利用导数先求出函数f(x)在区间[0,3]上的极大值,再求出区间端点的函数值,进行比较,得出最大值.又已知要求的问题:对于任意的x∈[0,3],都有f(x)<c2成立?f(x)max<c2,x∈[0,3].进而解出即可.
解答 解:(1)∵函数f(x)=2x3+3ax2+3bx+8c,
∴f′(x)=6x2+6ax+3b.
∵函数f(x)在x=1及x=2时取得极值,
∴$\left\{\begin{array}{l}{f′(1)=6+6a+3b=0}\\{f′(2)=24+12a+3b=0}\end{array}\right.$,解得 $\left\{\begin{array}{l}{a=-3}\\{b=4}\end{array}\right.$.
∴f′(x)=6x2-18x+12=6(x-1)(x-2).
经验证当a=-3,b=4时,函数f(x)在x=1及x=2时取得极值.
∴a=-3,b=4;
(2)由(1)可知:f′(x)=6x2-18x+12=6(x-1)(x-2).
令f′(x)=0,解得x=1,2,
令f′(x)>0,解得:x>2或x<1,令f′(x)<0,解得:1<x<2,
故函数f(x)在区间[0,1),(2,3]上单调递增;在区间(1,2)上单调递减.
∴函数f(x)在x=1处取得极大值,且f(1)=5+8c.
而f(3)=9+8c,∴f(1)<f(3),
∴函数f(x)在区间[0,3]上的最大值为f(3)=9+8c.
对于任意的x∈[0,3],都有f(x)<c2成立?f(x)max<c2,x∈[0,3]?9+8c<c2,
由c2-8c-9>0,解得c>9或c<-1.
∴要求的c的取值范围是(-∞,-1)∪(9,+∞).
点评 充分利用导数求函数的极值及对要求的问题正确转化是解题的关键.

 如图阴影部分是由曲线y=2x2和x2+y2=3及x轴围成的部分封闭图形,则阴影部分的面积为( )
如图阴影部分是由曲线y=2x2和x2+y2=3及x轴围成的部分封闭图形,则阴影部分的面积为( )| A. | $\frac{π}{2}-\frac{{\sqrt{3}}}{8}$ | B. | $\frac{π}{2}-\frac{{3\sqrt{3}}}{8}$ | C. | $\frac{3π}{2}-\frac{{\sqrt{3}}}{8}$ | D. | $\frac{3π}{2}-\frac{{3\sqrt{3}}}{8}$ |
| A. | 180 | B. | 200 | C. | 128 | D. | 162 |
(1)若命题“p或q”为真命题,则命题“p”和命题“q”均为真命题;
(2)命题“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1≤3x”;
(3)“x=4”是“x2-3x-4=0”的必要不充分条件;
(4)命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0”
| A. | (2)(3) | B. | (1)(2)(3) | C. | (2)(4) | D. | (2)(3)(4) |
| A. | 都平行 | B. | 都相交 | ||
| C. | 在两平面内 | D. | 至少和其中一个平行 |
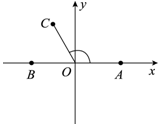 在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.
在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.