题目内容
用三段论证明,并指出每一步推理的大前提和小前提.
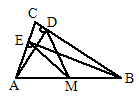
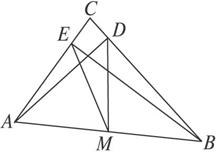
如图所示,在锐角三角形ABC中,AD⊥BC,BE⊥AC,D、E是垂足.求证:AB的中点M到D、E的距离相等.
答案:
解析:
解析:
|
证明:(1)因为有一个内角是直角的三角形是直角三角形,大前提 在△ABD中,AD⊥BC,即∠ADB=90°,小前提 所以△ABD是直角三角形.结论 同理,△AEB也是直角三角形. (2)因为直角三角形斜边上的中线等于斜边的一半,大前提 而M是Rt△ABD斜边AB的中点,DM是斜边上的中线,小前提 所以DM= 同理,EM= |

练习册系列答案
相关题目