题目内容
已知平面向量
=（
，-1），
=（sinx，cosx）（1）若已知
⊥
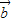，求tanx的值（2）若已知f（x）=
•
，求f（x）的最大值及取得最大值的x的取值集合．
【答案】分析：（1）利用两个向量垂直的性质，可得
，从而求得 tanx的值．
（2）化简f（x）的 解析式为
，故当
时，f（x）取的最大值2．
解答：解：（1）∵
⊥
，∴
•
=0，∴
，∴
．
（2）
=2
=
，
故当
时，即
，f（x）max=2．
点评：本题考查两个向量的数量积公式，两个向量垂直的性质，以及正弦函数的最大值，化简f（x）的 解析式是解题的关键．
，从而求得 tanx的值．（2）化简f（x）的 解析式为
，故当时，f（x）取的最大值2．解答：解：（1）∵
⊥，∴•=0，∴，∴．（2）
=2=，故当
时，即，f（x）max=2．点评：本题考查两个向量的数量积公式，两个向量垂直的性质，以及正弦函数的最大值，化简f（x）的 解析式是解题的关键．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
已知平面向量
=（1，-3），
=（4，-2），λ
+
与
垂直，则λ是（ ）
| a |
| b |
| a |
| b |
| a |
| A、-1 | B、1 | C、-2 | D、2 |
已知平面向量
，
满足|
|=1，|
|=2，
与
的夹角为60°，则“m=1”是“(
-m
)⊥
”的（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |