题目内容
如图,在四面体ABCD中,E、G分别为BC、AB的中点,F在CD上,H在AD上,且有DF∶FC=DH∶HA=2∶3,求证:EF、GH、BD交于一点.?
思路解析:本题证明时可以首先证明GH和EF共面交于一点O,然后说明O是平面ABD和平面BCD的公共点.平面ABD和平面BCD相交于直线BD,根据公理2,两平面相交,有且只有一条交线.因此,点O在直线BD上,直线EF、GH、BD都过点O.在该题中还涉及到证明E、F、H、G四点共面的问题,可利用公理3的推论.?
证明:∵E、G分别为BC、AB的中点,∴GE∥AC.?
又∵DF∶FC=DH∶HA=2∶3,∴FH∥AC.?
从而FH∥GE.故E、F、H、G四点共面.?
∵AG∶GB=1∶1,AH∶HD=3∶2,∴AG∶GB≠AH∶HD.?
∴GH不平行于BD.同理,EF也不平行于BD.?
∵GH∥EF,∴四边形EFHG是一个梯形,GH和EF交于一点O.?
∵O既在平面ABD内,又在平面BCD内,∴O在这两平面的交线上.?
又这两个平面的交线是BD,且交线只有这一条.?
∴点O在直线BD上.∴EF、GH、BD交于一点.
方法归纳 证明三线共点常用的方法是先说明两条直线共面且相交于一点,然后说明这个点在两个平面上,并且这两个平面相交,于是得到交线也过此点,从而得到三线共点.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
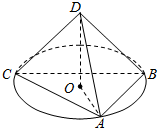 如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )
如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )A、[0,
| ||||
B、[0,
| ||||
C、[0,
| ||||
D、[0,
|
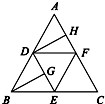 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为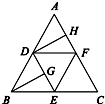 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )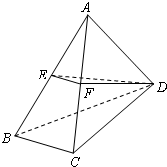 如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.
如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.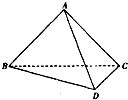 (2009•武汉模拟)如图,在四面体A-BCD中,
(2009•武汉模拟)如图,在四面体A-BCD中,