题目内容
用数学归纳法证明:当n是不小于5的自然数时,总有2n>n2成立.
证明:(1) 当n=5时,25>52,结论成立.
(2) 假设当n=k(k∈N,k≥5)时,结论成立,即有2k>k2,
那么当n=k+1时,左边=2k+1=2·2k>2·k2=(k+1)2+(k2-2k-1)=(k+1)2+(k-1- )(k-1+
)(k-1+ )>(k+1)2=右边.
)>(k+1)2=右边.
∴ 也就是说,当n=k+1时,结论成立.
∴ 由(1)、(2)可知,不等式 2n>n2对n∈N,n≥5时恒成立.

练习册系列答案
相关题目
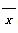 甲、
甲、
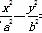 =1和椭圆
=1和椭圆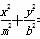 =1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
=1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( ) =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4 .
.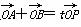 (O为坐标原点),当
(O为坐标原点),当 <
<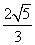 时,求实数t的取值范围.
时,求实数t的取值范围.
 =1在(x,y)→(x′,y′)=(x+2y,y)对应的变换下变换成另一个图形F′,试求F′的解析式.
=1在(x,y)→(x′,y′)=(x+2y,y)对应的变换下变换成另一个图形F′,试求F′的解析式.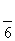 .
.