题目内容

已知椭圆的焦点是F1(0,-1)和F2(0,1),离心率e=.

(1)求椭圆的方程;

(2)又设点P在这个椭圆上,且|PF1|-|PF2|=1,求∠F1PF2的余弦值.

解:(1)∵c=1,e=,∴a=2,b2=a2-c2=3.

又椭圆中心在原点,焦点在y轴上,

∴椭圆的方程为.

(2)由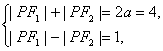解得|PF1|=,|PF2|=.

又|F1F2|=2c=2,

∴cos∠F1PF2=

即∠F1PF2的余弦值为.

练习册系列答案
相关题目
3、已知椭圆的焦点是F1、F2，P是椭圆上的一个动点，如果延长F1P到Q，使得|PQ|=|PF2|，那么动点Q的轨迹是（　　）
7、已知椭圆的焦点是F1、F2，P是椭圆上的一个动点，过点F2向∠F1PF2的外角平分线作垂线，垂足为M，则点M的轨迹是（　　）
已知椭圆的焦点是F1（-1，0），F2（1，0），P为椭圆上一点，且|F1F2|是|PF1|和|PF2|的等差中项．
（Ⅰ）求椭圆的方程；
（Ⅱ）求△PF1F2面积的最大值及此时点P的坐标．
已知椭圆的焦点是F1（0，-1）和F2（0，1），离心率e=
12
，
（I）求此椭圆的标准方程；
（Ⅱ）设点P在此椭圆上，且有|PF1|-|PF2|=1，求∠F1PF2的余弦值．
已知椭圆的焦点是F1，F2，P是椭圆上的一个动点，如果延长F1P到Q，使得|PQ|=|PF2|，那么动点Q的轨迹是（　　）
A、椭圆B、双曲线的一支C、抛物线D、圆

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网