题目内容
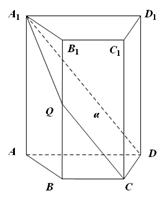
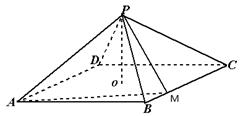
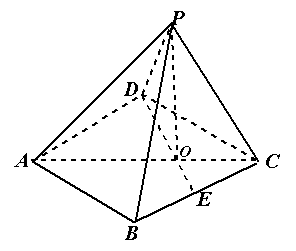
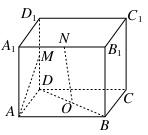
如图,四棱锥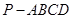 中,底面是以
中,底面是以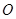 为中心的菱形,
为中心的菱形,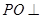 底面
底面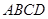 ,
,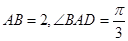 ,
,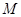 为
为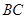 上一点,且
上一点,且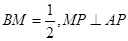 .
.
(1)求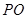 的长;
的长;
(2)求二面角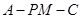 的正弦值.
的正弦值.
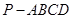 中,底面是以
中,底面是以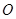 为中心的菱形,
为中心的菱形,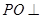 底面
底面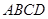 ,
,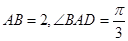 ,
,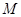 为
为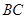 上一点,且
上一点,且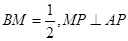 .
.(1)求
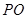 的长;
的长;(2)求二面角
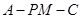 的正弦值.
的正弦值.
(1) ;(2)
;(2)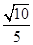 .
.
 ;(2)
;(2)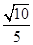 .
.试题分析:(1)连结
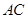 、
、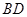 ,因为是菱形
,因为是菱形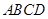 的中心,
的中心,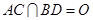 ,以
,以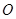 为坐标原点,
为坐标原点,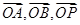 的方向分别为
的方向分别为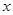 轴、
轴、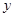 轴、
轴、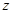 轴的正方向,建立空间直角坐标系,根据题设条件写出
轴的正方向,建立空间直角坐标系,根据题设条件写出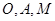 的坐标,并设出点
的坐标,并设出点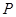 的坐标
的坐标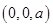 ,根据空间两点间的距离公式和勾股定理列方程解出
,根据空间两点间的距离公式和勾股定理列方程解出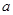 的值得到
的值得到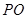 的长;.
的长;.(2)设平面
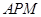 的法向量为
的法向量为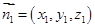 ,平面PMC的法向量为
,平面PMC的法向量为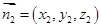 ,首先利用向量的数量积列方程求出向量
,首先利用向量的数量积列方程求出向量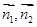 的坐标,再利用向量的夹角公式求出
的坐标,再利用向量的夹角公式求出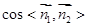 ,进而求出二面角
,进而求出二面角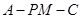 的正弦值.
的正弦值.解:
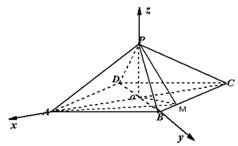
(1)如图,连结
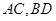 ,因
,因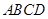 为菱形,则
为菱形,则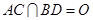 ,且
,且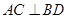 ,以
,以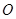 为坐标原点,
为坐标原点,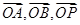 的方向分别为
的方向分别为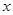 轴,
轴,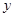 轴,
轴,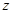 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系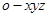 ,
,因
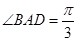 ,故
,故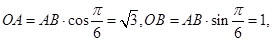
所以
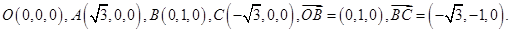
由
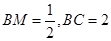 知,
知,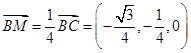
从而
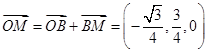 ,即
,即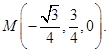
设
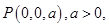 ,则
,则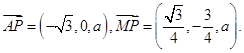 因为
因为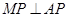 ,
,故
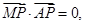 即
即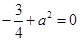 ,所以
,所以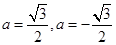 (舍去),即
(舍去),即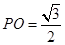 .
.(2)由(1)知,
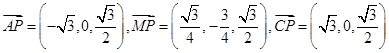 ,
,设平面
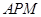 的法向量为
的法向量为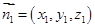 ,平面
,平面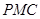 的法向量为
的法向量为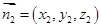
由
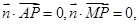 得
得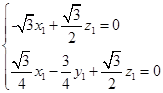 故可取
故可取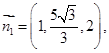
由
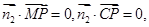 得
得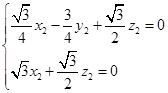 故可取
故可取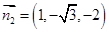
从而法向量
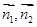 的夹角的余弦值为
的夹角的余弦值为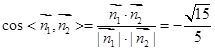
故所求二面角
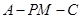 的正弦值为
的正弦值为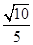 .
.
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
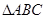 和
和 所在平面互相垂直,且
所在平面互相垂直,且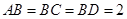 ,
,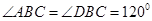 ,E、F分别为AC、DC的中点.
,E、F分别为AC、DC的中点.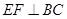 ;
;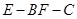 的正弦值.
的正弦值.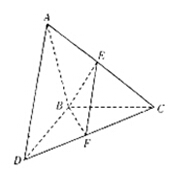
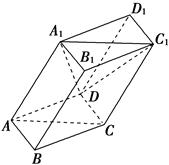
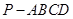 的底面的菱形,
的底面的菱形,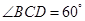 ,点
,点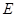 是
是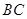 边的中点,
边的中点,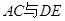 交于点
交于点 ,
,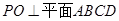
 ;
;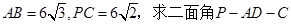 的大小;
的大小;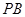 与
与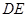 所成角的余弦值。
所成角的余弦值。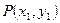 、
、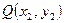 之间的“直角距离”为
之间的“直角距离”为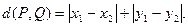 若
若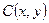 到点
到点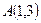 、
、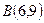 的“直角距离”相等,其中实
的“直角距离”相等,其中实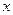 、
、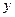 满足
满足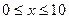 、
、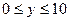 ,则所有满足条件的点
,则所有满足条件的点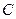 的轨迹的长度之和为 .
的轨迹的长度之和为 .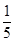
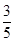
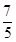
 、
、 夹角θ的余弦值为( )
夹角θ的余弦值为( )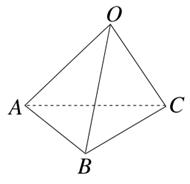
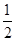
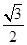
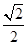
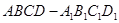 中,
中,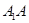
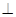 底面
底面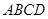 .四边形
.四边形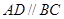 ,且
,且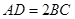 .过
.过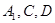 三点的平面记为
三点的平面记为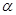 ,
,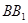 与
与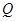 .
.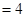 ,
,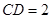 ,梯形
,梯形