题目内容
已知两个正数a,b的等差中项为4,则a,b的等比中项的最大值为( )
| A.2 | B.4 | C.8 | D.16 |
B
解析试题分析:由等差中项的定义得到关于a、b的关系式,再根据均值不等式化简即可得到关于a、b的等比中项的不等式,即可求最大值解:∵a、b的等差中项为4,∴a+b=8,又∵a、b是正数∴a+b≥2 (a=b时等号成立)∴
(a=b时等号成立)∴ ≤4,又由等比中项的定义知a、b的等比中项为±
≤4,又由等比中项的定义知a、b的等比中项为± ,∴a、b的等比中项的最大值为4,故选B
,∴a、b的等比中项的最大值为4,故选B
考点:等差中项和等比中项
点评:本题考查等差中项和等比中项的定义和均值不等式,要注意两个数的等比中项有两个,同时要注意均值不等式的条件.属简单题

练习册系列答案
相关题目
数列 等比数列,
等比数列, ,
, ,则数列
,则数列 的前
的前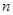 项的和为( )
项的和为( )
A. | B. | C. | D. |
各项均为正数的等比数列 的前
的前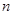 项和为
项和为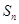 ,若
,若 ,
, ,则
,则 等于( )
等于( )
| A.80 | B.30 | C.26 | D.16 |
等比数列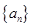 中,
中, ,
, =4,函数
=4,函数 ,则
,则 ( )
( )
A. | B. | C. | D. |
已知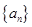 是首项为
是首项为 的等比数列,
的等比数列, 是
是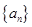 的前
的前 项和,且
项和,且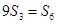 .则
.则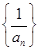 的前
的前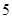 项和为.
项和为.
A. 或 或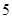 | B.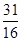 或 或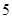 | C.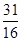 | D. |
在等差数列 中,公差d >0,
中,公差d >0, 是方程
是方程 的两个根,
的两个根, 是数列
是数列 的前n项的和,那么满足条件
的前n项的和,那么满足条件 >0的最小自然数n=( )
>0的最小自然数n=( )
| A.4018 | B.4017 | C.2009 | D.2010 |
已知数列 的前
的前 项和为
项和为 ,
, ,
, ,则
,则 的值为
的值为
A. | B. | C. | D. |
已知正项等比数列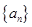 满足:
满足: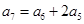 ,若存在两项
,若存在两项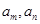 使得
使得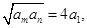 则
则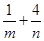 的最小值为( ).
的最小值为( ).
A.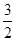 | B.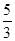 | C.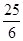 | D.不存在 |
等比数列{an}的前n项和为Sn,已知S3 = a2 +10a1 ,a5 = 9,则a1=( )
A. | B.-  |
C. | D.-  |