题目内容
(满分12分)如图,在长方体![]() 中,
中,![]()
![]() 分别是棱
分别是棱![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() ,
,
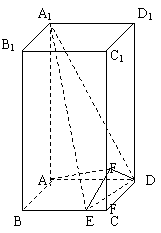 (1)求异面直线
(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)证明![]()
![]() 平面
平面![]() ;
;
(3)求二面角![]() 的正弦值。
的正弦值。
以点A为坐标原点建立空间直角坐标系,设![]() ,依题意得
,依题意得
![]() ,
,![]() ,
,![]() ,
,![]()
(1)易得![]() ,
,![]() ,于是
,于是
所以异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() 。 (4分)
。 (4分)
(2)证明:易知![]() ,
,
于是![]() ,因此
,因此![]() ,
,![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() 。 (8分)
。 (8分)
(3)解:设平面![]() 的法向量
的法向量![]()
则![]()
 即
即![]()

不妨令X=1,可得![]() 由(2)可知,
由(2)可知,![]() 为平面
为平面![]() 的一个法向量。
的一个法向量。
于是 ,从而
,从而![]() ,
,
所以二面角![]() 的正弦值为
的正弦值为![]() (12分)
(12分)

练习册系列答案
相关题目
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线 是以直线AD为对称轴,以线段
是以直线AD为对称轴,以线段 的中点
的中点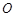 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线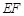 ,可使剩余的直角梯形的面积最大?并求其最大值.
,可使剩余的直角梯形的面积最大?并求其最大值.
 中,
中, ,
, ,
, ,平面
,平面 平面
平面 ,
, 是线段
是线段 上一点,
上一点, ,
, ,
, .
. 平面
平面 ;
; 与四棱锥
与四棱锥 与
与 ,求
,求 的值.
的值.

 的中点,P为BB1的中点.
的中点,P为BB1的中点. ;
; 所成角的大小;
所成角的大小;