题目内容

已知曲线C的方程是x2+y2=k,则当k为何值时,直线y=2x-5与C有两个交点？只有一个交点？没有交点？

思路解析：曲线的交点个数就是方程组解的个数.

解：由题意得,

∴x2+(2x-5)2=k.

∴5x2-20x+25-k=0.

则有Δ=400-20(25-k)=20k-100.

∴当Δ＞0,即k＞5时,有两个交点；

当Δ=0,即k=5时,只有一个交点；

当Δ＜0,即k＜5,也即0＜k＜5时,没有交点.

深化升华

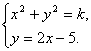
    曲线C1:f(x,y)=0与曲线C2:g(x,y)=0的交点个数与方程组解的个数相同.

练习册系列答案
相关题目
已知一点P的坐标是（4，-2），直线L的方程是y-x+5=0，曲线C的方程是
(x+1)2
2
+
(y-1)2
4
=1，求经过P点而与L垂直的直线和曲线C的交点的坐标．
已知曲线C的方程为x2+x+y-1=0，则下列各点中在曲线C上的点是（　　）
已知曲线C的方程为y2=4x（x＞0），曲线E是以F1（-1，0）、F2（1，0）为焦点的椭圆，点P为曲线C与曲线E在第一象限的交点，且|PF2|=
53
．
（1）求曲线E的标准方程；
（2）直线l与椭圆E相交于A，B两点，若AB的中点M在曲线C上，求直线l的斜率k的取值范围．
（2012•西城区二模）已知曲线C的方程是(x-
|x|
x
)2+(y-
|y|
y
)2=8，给出下列三个结论：
①曲线C与两坐标轴有公共点；
②曲线C既是中心对称图形，又是轴对称图形；
③若点P，Q在曲线C上，则|PQ|的最大值是6
2
．
其中，所有正确结论的序号是
②③
②③
．

已知曲线C的方程是(t＋1)＋2at)x＋3at＋b＝0，直线l的

方程是y＝t(x－1)，若对任意实数t，曲线C恒过定点P(1，0)．

(1)求定值a，b；

(2)直线l截曲线C所得弦长为d，记f(t)＝，则当t为何值时，f(t)有最大值，最大值是多少？

(3)若点M()在曲线C上，又在直线l上，求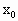的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网