题目内容
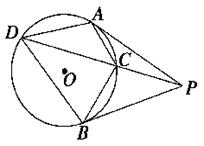
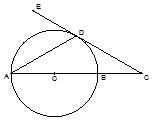
(12分)从⊙O外一点P引圆的两条切线PA,PB及一条割线PCD,A,B为切点.
求证: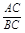 =
=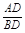 .
.

求证:
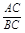 =
=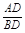 .
.见解析。
从⊙O外一点P引圆的两条切线PA,PB,则 ,根据弦切角等于圆周角,可证出
,根据弦切角等于圆周角,可证出 与
与 相似,
相似, 与
与 相似,对应边成比例,即证得结论.
相似,对应边成比例,即证得结论.
∵PA为⊙O的切线,∴∠PAC=∠PDA,
而∠APC=∠DPA,∴△PAC∽△PDA,
则 =
= .同理
.同理 =
= .
.
∵PA=PB,∴ =
= .∴
.∴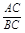 =
=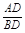 .
.
 ,根据弦切角等于圆周角,可证出
,根据弦切角等于圆周角,可证出 与
与 相似,
相似, 与
与 相似,对应边成比例,即证得结论.
相似,对应边成比例,即证得结论.∵PA为⊙O的切线,∴∠PAC=∠PDA,
而∠APC=∠DPA,∴△PAC∽△PDA,
则
 =
= .同理
.同理 =
= .
.∵PA=PB,∴
 =
= .∴
.∴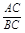 =
=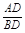 .
.
练习册系列答案
相关题目
 内切于点T,P是外圆
内切于点T,P是外圆 上任意一点,连PT交
上任意一点,连PT交 于点M,PN与内圆
于点M,PN与内圆
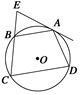
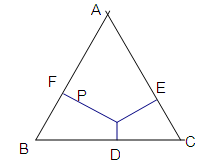
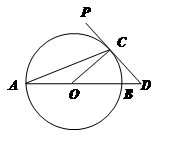
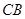 是⊙
是⊙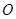 的直径,
的直径,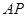 是⊙
是⊙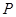 ,
,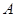 为切点.若
为切点.若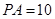 ,
,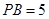 ,
,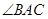 的平分线
的平分线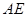 与
与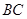 和⊙
和⊙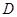 、
、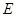 ,则
,则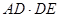 的值为( )
的值为( )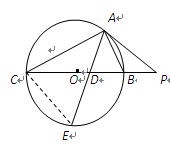
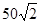
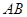 ="6" cm,
="6" cm,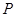 是
是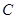 ,连接
,连接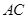 , 若
, 若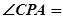 30°,PB的长为( )cm.
30°,PB的长为( )cm.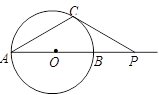
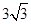
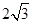
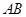 是⊙
是⊙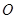 的直径,直线
的直径,直线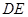 切⊙
切⊙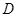 ,且与
,且与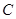 ,若
,若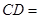
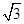 ,
,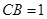 ,则
,则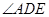 = .
= .
 为圆
为圆 外一点,由
外一点,由 与圆
与圆 切于
切于 点,引圆
点,引圆 与圆
与圆 点.已知
点.已知 ,
, .则圆
.则圆