题目内容
如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且二面角A-DC-E为直二面角.
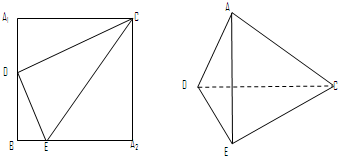
(1)求证:CD⊥DE;
(2)求AE与面DEC所成的角.

(1)求证:CD⊥DE;
(2)求AE与面DEC所成的角.
分析:(1)由折叠后正方形的直角顶点A1,A2重合于A,可由线面垂直的判定定理证得AC⊥面ADE,进而得到A-DC-E为直二面角,过A作AF⊥CD于F,由面面垂直的性质定理可得AF⊥面CDE,进而得到AF⊥DE,再由线面垂直的判定定理得到DE⊥面ACD后,可得答案.
(2)由(1)中AF⊥面CDE,可得∠AEF为AE与面DEC所成的角,解Rt△CAD,可求出AF,解Rt△ADE可求出AE,解Rt△AFE可得答案.
(2)由(1)中AF⊥面CDE,可得∠AEF为AE与面DEC所成的角,解Rt△CAD,可求出AF,解Rt△ADE可求出AE,解Rt△AFE可得答案.
解答: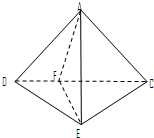 证明:(1)∵A1,A2重合于A,
证明:(1)∵A1,A2重合于A,
∴AC⊥AD,AC⊥AE,故AC⊥面ADE,
∴AC⊥DE,由于A-DC-E为直二面角,
过A作AF⊥CD于F,则AF⊥面CDE
∴AF⊥DE,AC∩AF=A
∴DE⊥面ACD,
∴CD⊥DE(3分)
解:(2)∵AF⊥面CDE,
∴∠AEF为AE与面DEC所成的角,
在Rt△CAD中,AD=2AC=4,
∴DC=2
,AF=
又CD⊥DE
∴在正方形A1BA2C中,△DBE与△CA1D相似
故
=
⇒BE=1(2分)
∴在Rt△ADE中,AE=3,
故在Rt△AFE中,sin∠AFE=
=
∴AE与面DEC所成的角为arcsin
(3分)
 证明:(1)∵A1,A2重合于A,
证明:(1)∵A1,A2重合于A,∴AC⊥AD,AC⊥AE,故AC⊥面ADE,
∴AC⊥DE,由于A-DC-E为直二面角,
过A作AF⊥CD于F,则AF⊥面CDE
∴AF⊥DE,AC∩AF=A
∴DE⊥面ACD,
∴CD⊥DE(3分)
解:(2)∵AF⊥面CDE,
∴∠AEF为AE与面DEC所成的角,
在Rt△CAD中,AD=2AC=4,
∴DC=2
| 5 |
| 4 | ||
|
又CD⊥DE
∴在正方形A1BA2C中,△DBE与△CA1D相似
故
| A1C |
| A1D |
| BD |
| BE |
∴在Rt△ADE中,AE=3,
故在Rt△AFE中,sin∠AFE=
| AF |
| AE |
4
| ||
| 15 |
∴AE与面DEC所成的角为arcsin
4
| ||
| 15 |
点评:本题考查的知识点是直线与平面所成的角,直线与平面垂直的性质,熟练掌握线线垂直,线面垂直,面面垂直之间的转化及线面夹角的定义是解答本题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 w_w w. k#s5_u.c o*m
w_w w. k#s5_u.c o*m
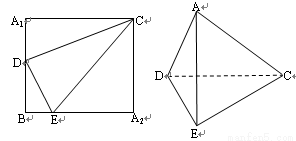
 (1)求证:CD⊥DE;
(1)求证:CD⊥DE;
