题目内容
求同时满足下列两个条件的所有复数z:①z+
| 10 |
| z |
| 10 |
| z |
②z的实部和虚部都是整数.
分析:根据题意,对于①从整体角度思考,可视z+
为一个整体t,进行整体换元,得到 z2-tz+10=0,对于②利用求根公式解出 z,再利用z的实部和虚部都是整数,求出t,即得满足条件的复数z.
| 10 |
| z |
解答:解:设z+
=t,则 z2-tz+10=0.∵1<t≤6,∴△=t2-40<0,
解方程得 z=
±
i.
又∵z的实部和虚部都是整数,∴t=2或t=6,
故满足条件的复数共4个:z=1±3i 或 z=3±i.
| 10 |
| z |
解方程得 z=
| t |
| 2 |
| ||
| 2 |
又∵z的实部和虚部都是整数,∴t=2或t=6,
故满足条件的复数共4个:z=1±3i 或 z=3±i.
点评:本题考查一元二次方程在判别式小于0时的解法,体现了换元的思想.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
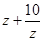 是实数,且
是实数,且 ;
; 的实部和虚部都是整数.
的实部和虚部都是整数.