题目内容
已知Sn是正项数列{an}的前n项和，且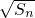
是
与（an+1）2的等比中项．
（1）求证：数列{an}是等差数列；
（2）若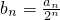
，求数列{bn}的前n项和Tn；
（3）若
对一切正整数n恒成立，求实数m的取值范围．
解：（1）当 n≥2时，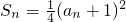
，
两式相减，整理得（an+an-1）（an-an-1-2）=0，由于数列{an}是正项数列，∴an-an-1=2，又a1=1，所以数列{an}是首项a1=1，d=2的等差数列，an=2n-1；
（2）
，
相减化简得
（3）∵
当n=1，b2＞b1，当n≥2，bn+1＜bn，故当n=2时，b2取到最大值
．
又对一切正整数n恒成立，即
解得m≤-1或m≥5
分析：（1）由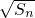是与（an+1）2的等比中项，可得
，两式相减可求．
（2），故用裂项求和法求解；
（3）先求数列{bn}的最大值，进而转化为解不等式．从而求出参数范围．
点评：本题主要考查等差数列的定义，裂项求和法及借助于最值解决恒成立问题，属于中档题．
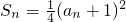
，两式相减，整理得（an+an-1）（an-an-1-2）=0，由于数列{an}是正项数列，∴an-an-1=2，又a1=1，所以数列{an}是首项a1=1，d=2的等差数列，an=2n-1；
（2）
，相减化简得
（3）∵
当n=1，b2＞b1，当n≥2，bn+1＜bn，故当n=2时，b2取到最大值
．又
对一切正整数n恒成立，即解得m≤-1或m≥5
分析：（1）由
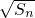是与（an+1）2的等比中项，可得，两式相减可求．（2）
，故用裂项求和法求解；（3）先求数列{bn}的最大值，进而转化为解不等式
．从而求出参数范围．点评：本题主要考查等差数列的定义，裂项求和法及借助于最值解决恒成立问题，属于中档题．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
已知Sn是正项数列an的前n项和，且an+
=2Sn，那么an的通项公式为（ ）
| 1 |
| an |
A、an=
| ||||
B、an=
| ||||
C、an=
| ||||
D、an=
|
是
与（an+1）2的等比中项．
，求数列{bn}的前n项和Tn；
对一切正整数n恒成立，求实数m的取值范围．