题目内容
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示.
假设每名队员每次射击相互独立.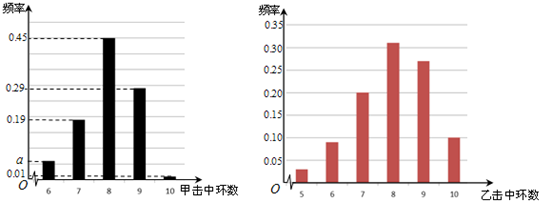
(Ⅰ)求上图中a的值;
(Ⅱ)队员甲进行三次射击,求击中目标靶的环数不低于8环的次数X的分布列及数学期望(频率当作概率使用);
(Ⅲ)由上图判断,在甲、乙两名队员中,哪一名队员的射击成绩更稳定?(结论不需证明)
假设每名队员每次射击相互独立.

(Ⅰ)求上图中a的值;
(Ⅱ)队员甲进行三次射击,求击中目标靶的环数不低于8环的次数X的分布列及数学期望(频率当作概率使用);
(Ⅲ)由上图判断,在甲、乙两名队员中,哪一名队员的射击成绩更稳定?(结论不需证明)
分析:(Ⅰ)根据所有频率和为1建立等式,可求出a的值;
(Ⅱ)先求队员甲进行三次射击,击中目标靶的环数不低于8环的概率,随机变量X的取值为:0,1,2,3,然后分别求出相应的概率,列出分布列,最后利用数学期望公式解之即可;
(Ⅲ)在甲、乙两名队员中,通过频率分布情况看队员的射击成绩哪个相对集中,那就更稳定.
(Ⅱ)先求队员甲进行三次射击,击中目标靶的环数不低于8环的概率,随机变量X的取值为:0,1,2,3,然后分别求出相应的概率,列出分布列,最后利用数学期望公式解之即可;
(Ⅲ)在甲、乙两名队员中,通过频率分布情况看队员的射击成绩哪个相对集中,那就更稳定.
解答:解:(Ⅰ)由上图可得0.01+a+0.19+0.29+0.45=1,
∴a=0.06;
(Ⅱ)由图可得队员甲击中目标靶的环数不低于8环的概率为0.45+0.29+0.01=0.75,
由题意可知随机变量X的取值为:0,1,2,3,
事件“X=k”的含义是在3次射击中,恰有k次击中目标靶的环数不低于8环,
P(X=k)=
(
)k(1-
)3-k(k=0,1,2,3),
即X的分布列为
所以X的期望是E(X)=0×
+1×
+2×
+3×
=
;
(Ⅲ)甲队员的射击成绩更稳定.
∴a=0.06;
(Ⅱ)由图可得队员甲击中目标靶的环数不低于8环的概率为0.45+0.29+0.01=0.75,
由题意可知随机变量X的取值为:0,1,2,3,
事件“X=k”的含义是在3次射击中,恰有k次击中目标靶的环数不低于8环,
P(X=k)=
| C | k 3 |
| 3 |
| 4 |
| 3 |
| 4 |
即X的分布列为
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 64 |
| 9 |
| 64 |
| 27 |
| 64 |
| 27 |
| 64 |
| 9 |
| 4 |
(Ⅲ)甲队员的射击成绩更稳定.
点评:本题主要考查了频率分布情况,以及分布列及数学期望,同时考查了n次独立重复试验的概率,考查运算求解的能力,属于中档题.

练习册系列答案
相关题目
12分)
要从两名同学中挑出一名,代表班级参加射击比赛,根据以往的成绩记录同学甲击中目标的环数为X1的分布列为
|
X1 |
5 |
6 |
7 |
8 |
9 |
10 |
|
P |
0.03 |
0.09 |
0.20 |
0.31 |
0.27 |
0.10 |
同学乙击目标的环数X2的分布列为
|
X2 |
5 |
6 |
7 |
8 |
9 |
|
P |
0.01 |
0.05 |
0.20 |
0.41 |
0.33 |
(1)请你评价两位同学的射击水平(用数据作依据);
(2)如果其它班参加选手成绩都在9环左右,本班应派哪一位选手参赛,如果其它班参赛选手的成绩都在7环左右呢?
 根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示:
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示: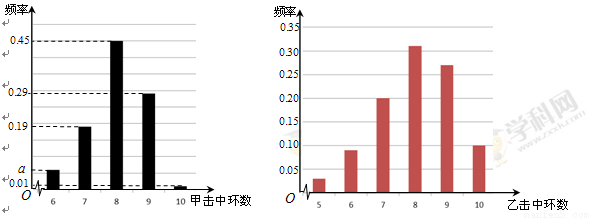
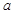 的值;
的值;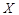 的分布列及数学期望(频率当作概率使用);
的分布列及数学期望(频率当作概率使用);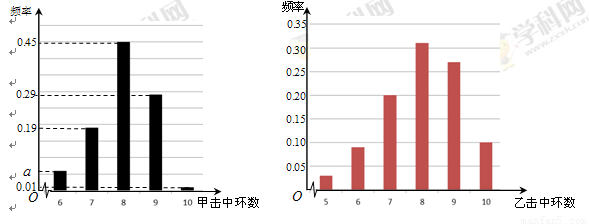
 的值;
的值;