题目内容
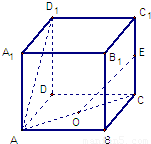如图，在正方体ABCD-A1B1C1D1中，O是底面ABCD的中心，E为CC1的中点，那么异面直线OE与AD1所成角的余弦值等于（ ）A．
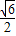
B．
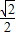
C．
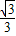
D．
【答案】分析：由正方体的结构特征，我们取BC的中点F，连接EF，OF，BC1，可证得∠OEF即为异面直线OE与AD1所成角，解△OEF即可得到答案．
解答：
解：取BC的中点F，连接EF，OF，BC1，如图所示：
∵E为CC1的中点，EF∥BC1∥AD1，
故∠OEF即为异面直线OE与AD1所成角
设正方体ABCD-A1B1C1D1的棱长为2，
则在△OEF中，EF=
，OE=
故cos∠OEF=
=
故选D
点评：本题考查的知识点是异面直线及其所成的角，其中根据正方体的几何特征，构造出异面直线OE与AD1所成角∠OEF是解答本题的关键．
解答：
解：取BC的中点F，连接EF，OF，BC1，如图所示：∵E为CC1的中点，EF∥BC1∥AD1，
故∠OEF即为异面直线OE与AD1所成角
设正方体ABCD-A1B1C1D1的棱长为2，
则在△OEF中，EF=
，OE=故cos∠OEF=
=故选D
点评：本题考查的知识点是异面直线及其所成的角，其中根据正方体的几何特征，构造出异面直线OE与AD1所成角∠OEF是解答本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
如图，在正方体ABCD-A1B1C1D1中，E为DD1的中点，
如图，在正方体ABCD-A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P-ABC的主视图与左视图的面积的比值为（ ）