题目内容
若△ABC的三个内角是A、B、C且A<B<C(C≠A.sinA<sinC B.cotA<cotC
C.tanA<tanC D.cosA<cosC
解析:因为A、B、C为△ABC的三个内角,所以存在C为钝角的可能,而A仍为锐角,此时结论仍然正确.而cosA、tanA、cotA均为正数,cosC、tanC、cotC均为负数,因此B、C、D均可排除.
答案:A}}
12{{题型:解答题;单元:4.6两角和与差的正弦、余弦、正切;知识点:两角和与差、二倍角的三角函数;难度:中;其它备注:主观题;分值:8$$已知tanα=![]() (1+m),
(1+m),![]() (tanα·tanβ+m)+tanβ=0且α、β均为锐角,求α+β.
(tanα·tanβ+m)+tanβ=0且α、β均为锐角,求α+β.
@@解: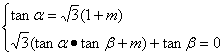
![]()
![]() tanα·tanβ+tanα+tanβ-
tanα·tanβ+tanα+tanβ-![]() =0,
=0,
tanα+tanβ-![]() (1-tanα·tanβ)=0.
(1-tanα·tanβ)=0.
∴tan(α+β)=![]() =
=![]() .
.
又∵0<α+β<π,
∴α+β=![]() .
.

练习册系列答案
相关题目
若△ABC的三个内角满足sinA:sinB:sinC=2:3:4,则△ABC( )
| A、一定是直角三角形 | B、一定是钝角三角形 | C、一定是锐角三角形 | D、可能是锐角三角形,也可能是钝角三角形 |