题目内容
直线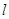 过点
过点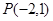 且斜率为
且斜率为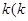 >
>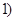 ,将直线
,将直线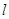 绕
绕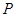 点按逆时针方向旋转45°得直线
点按逆时针方向旋转45°得直线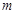 ,若直线
,若直线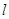 和
和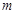 分别与
分别与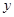 轴交于
轴交于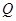 ,
,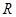 两点.(1)用
两点.(1)用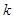 表示直线
表示直线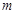 的斜率;(2)当
的斜率;(2)当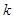 为何值时,
为何值时,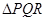 的面积最小?并求出面积最小时直线
的面积最小?并求出面积最小时直线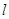 的方程.
的方程.
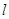 过点
过点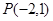 且斜率为
且斜率为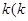 >
>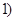 ,将直线
,将直线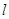 绕
绕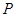 点按逆时针方向旋转45°得直线
点按逆时针方向旋转45°得直线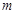 ,若直线
,若直线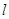 和
和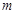 分别与
分别与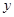 轴交于
轴交于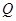 ,
,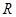 两点.(1)用
两点.(1)用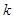 表示直线
表示直线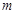 的斜率;(2)当
的斜率;(2)当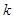 为何值时,
为何值时,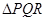 的面积最小?并求出面积最小时直线
的面积最小?并求出面积最小时直线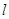 的方程.
的方程.(1) ,
,
(2)当 时,
时,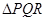 的面积最小,最小值为
的面积最小,最小值为 ,此时直线
,此时直线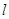 的方程是
的方程是 .
.
 ,
,(2)当
 时,
时,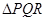 的面积最小,最小值为
的面积最小,最小值为 ,此时直线
,此时直线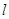 的方程是
的方程是 .
.本题考查一条直线到另一直线的角的定义,直线的点斜式方程,求两直线的交点坐标以及基本不等式的应用.把三角形的面积表达式变形后应用基本不等式是本题的难点和关键.
(1)用点斜式求出m和l的方程,利用直线l绕P点按逆时针方向旋转45°得直线m求出直线m的倾斜角为α+45°;进而得到直线m的斜率;
(2)求出R,Q两点的坐标,计算△PQR 的面积,变形后应用基本不等式求出它的最小值
(1)用点斜式求出m和l的方程,利用直线l绕P点按逆时针方向旋转45°得直线m求出直线m的倾斜角为α+45°;进而得到直线m的斜率;
(2)求出R,Q两点的坐标,计算△PQR 的面积,变形后应用基本不等式求出它的最小值

练习册系列答案
相关题目
 的直线,且使
的直线,且使 ,
, 到它的距离相等的直线方程.( )
到它的距离相等的直线方程.( )


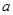 为常数,若曲线
为常数,若曲线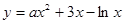 存在与直线
存在与直线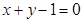 垂直的切线,则实数
垂直的切线,则实数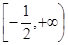
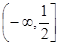
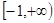
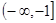
 经过
经过 两点,那么直线
两点,那么直线



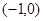 ,且与直线
,且与直线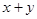 =0垂直的直线方程是
=0垂直的直线方程是  经过点
经过点 ,那么直线
,那么直线