Question

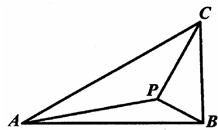如图，在△ABC中，∠ABC=90°，AB=

3

，BC=1，P为△ABC内一点，∠BPC=90°．
（1）若PC=

3

2

．求PA．
（2）若∠APB=120°，求tan∠PAB的值．

Answer 1

分析：（1）Rt△BPC中利用三角函数的定义，算出sin∠PBC=

3

2

，可得∠PBC=60°，从而BP=BCcos60°=

1

2

．再在△APB中算出∠PBA=30°，利用余弦定理加以计算即可得出PA的大小．
（2）设∠PBA=α，从而算出PB=sinα，∠PAB=60°-α．在△APB中根据正弦定理建立关于α的等式，解出2sinα=

3

cosα，利用同角三角函数的关系算出tanα=

3

2

，再由两角差的正切公式即可算出tan∠PAB的值．

解答：解：（1）∵在Rt△BPC中，PC=

3

2

，BC=1，
∴sin∠PBC=

PC

BC

=

3

2

，可得∠PBC=60°，BP=BCcos60°=

1

2

．
∵∠PBA=90°-∠PBC=30°，
∴△APB中，由余弦定理PA²=PB²+AB²-2PB•AB•cos∠PBA，
得PA²=

1

4

+3-2×

1

2

×

3

×

3

2

=

7

4

，解之得PA=

7

2

（舍负）．
（2）设∠PBA=α，可得∠PBC=90°-α，∠PAB=180°-∠PBA-∠APB=60°-α，
在Rt△BPC中，PB=BCcos∠PBC=cos（90°-α）=sinα，
△ABP中，由正弦定理得

AB

sin120°

=

PB

sin(60°-α)

，即

3

3 2

=

sinα

sin(60°-α)

，
∴sinα=2sin（60°-α）=2（

3

2

cosα-

1

2

sinα），化简得2sinα=

3

cosα，
由此可得tanα=

sinα

cosα

=

3

2

，所以tan∠PAB=tan（60°-α）=

3 - 3 2

1+ 3 × 3 2

=

3

5

．

点评：本题在直角三角形中求线段PA的长与角的正切值，着重考查了利用正余弦定理解三角形、同角三角函数的基本关系和两角和与差的三角公式等知识，属于中档题．