题目内容
已知数列{an}、{bn}满足: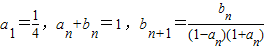 .
.(Ⅰ)求b1,b2,b3,b4;
(Ⅱ)设
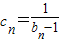 ,求数列{cn}的通项公式;
,求数列{cn}的通项公式;(Ⅲ)设Sn=a1a2+a2a3+a3a4+…+anan+1,不等式4aSn<bn恒成立时,求实数的取值范围.
【答案】分析:(Ⅰ) 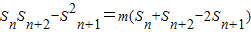 ,由[lg(Sn-m)+lg(Sn+2-m)]=2lg(Sn+1-m),能求出b1,b2,b3,b4.
,由[lg(Sn-m)+lg(Sn+2-m)]=2lg(Sn+1-m),能求出b1,b2,b3,b4.
(Ⅱ)由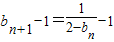 ,知
,知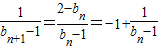 ,由此能求出cn.
,由此能求出cn.
(Ⅲ)由于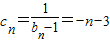 ,所以
,所以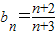 ,从而
,从而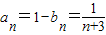 ,所以由条件知(a-1)n2+(3a-6)n-8<0恒成立即可满足条件,由此能够推导出a≤1时,4aSn<bn恒成立.
,所以由条件知(a-1)n2+(3a-6)n-8<0恒成立即可满足条件,由此能够推导出a≤1时,4aSn<bn恒成立.
解答:(本题14分)
解:(Ⅰ)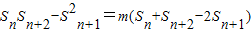 ,
,
∵[lg(Sn-m)+lg(Sn+2-m)]=2lg(Sn+1-m),
∴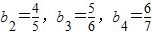 .…(4分)
.…(4分)
(Ⅱ)∵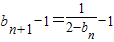 ,
,
∴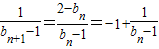 ,…(5分)
,…(5分)
∴数列{cn}是以-4为首项,-1为公差的等差数列.
∴cn=-4+(n-1)•(-1)=-n-3.…(7分)
(Ⅲ)由于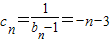 ,
,
所以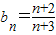 ,
,
从而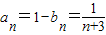 ..…(8分)
..…(8分)
∴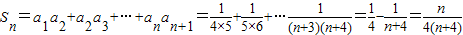
∴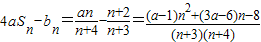 …(10分)
…(10分)
由条件知(a-1)n2+(3a-6)n-8<0恒成立即可满足条件,
设f(n)=(a-1)n2+(3a-6)n-8,
当a=1时,f(n)=-3n-8<0恒成立
当a>1时,由二次函数的性质知不可能成立,
当a<1时,对称轴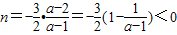 ,
,
f(n)在(1,+∞)为单调递减函数.
f(1)=(a-1)n2+(3a-6)n-8=(a-1)+(3a-6)-8=4a-15<0,
∴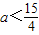 ,
,
∴a<1时4aSn<bn恒成立
综上知:a≤1时,4aSn<bn恒成立…(14分)
点评:本题考查数列的通项公式的求法,考查满足条件的实数的取值范围的求法.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
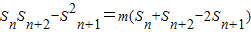 ,由[lg(Sn-m)+lg(Sn+2-m)]=2lg(Sn+1-m),能求出b1,b2,b3,b4.
,由[lg(Sn-m)+lg(Sn+2-m)]=2lg(Sn+1-m),能求出b1,b2,b3,b4.(Ⅱ)由
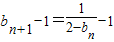 ,知
,知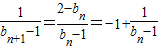 ,由此能求出cn.
,由此能求出cn.(Ⅲ)由于
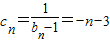 ,所以
,所以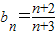 ,从而
,从而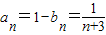 ,所以由条件知(a-1)n2+(3a-6)n-8<0恒成立即可满足条件,由此能够推导出a≤1时,4aSn<bn恒成立.
,所以由条件知(a-1)n2+(3a-6)n-8<0恒成立即可满足条件,由此能够推导出a≤1时,4aSn<bn恒成立.解答:(本题14分)
解:(Ⅰ)
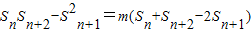 ,
,∵[lg(Sn-m)+lg(Sn+2-m)]=2lg(Sn+1-m),
∴
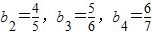 .…(4分)
.…(4分)(Ⅱ)∵
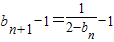 ,
,∴
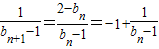 ,…(5分)
,…(5分)∴数列{cn}是以-4为首项,-1为公差的等差数列.
∴cn=-4+(n-1)•(-1)=-n-3.…(7分)
(Ⅲ)由于
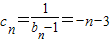 ,
,所以
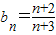 ,
,从而
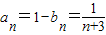 ..…(8分)
..…(8分)∴
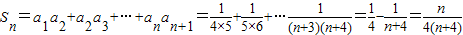
∴
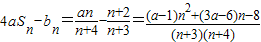 …(10分)
…(10分)由条件知(a-1)n2+(3a-6)n-8<0恒成立即可满足条件,
设f(n)=(a-1)n2+(3a-6)n-8,
当a=1时,f(n)=-3n-8<0恒成立
当a>1时,由二次函数的性质知不可能成立,
当a<1时,对称轴
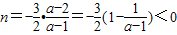 ,
,f(n)在(1,+∞)为单调递减函数.
f(1)=(a-1)n2+(3a-6)n-8=(a-1)+(3a-6)-8=4a-15<0,
∴
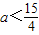 ,
,∴a<1时4aSn<bn恒成立
综上知:a≤1时,4aSn<bn恒成立…(14分)
点评:本题考查数列的通项公式的求法,考查满足条件的实数的取值范围的求法.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
相关题目