题目内容
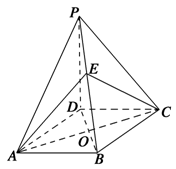
如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=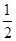 PD.
PD.
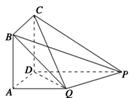
(1)求证:平面PQC⊥平面DCQ;
(2)若二面角Q-BP-C的余弦值为-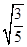 ,求
,求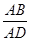 的值.
的值.
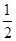 PD.
PD.
(1)求证:平面PQC⊥平面DCQ;
(2)若二面角Q-BP-C的余弦值为-
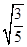 ,求
,求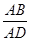 的值.
的值.(1)见解析(2)1
(1)证明:设AD=1,则DQ=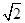 ,DP=2,又∵PD∥QA,∴∠PDQ=∠AQD=45°,在△DPQ中,由余弦定理可得PQ=
,DP=2,又∵PD∥QA,∴∠PDQ=∠AQD=45°,在△DPQ中,由余弦定理可得PQ=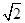 .
.
∴DQ2+PQ2=DP2,∴PQ⊥DQ,又∵PD⊥平面ABCD,∴PD⊥DC,∵CD⊥DA,DA∩PD=D,∴CD⊥平面ADPQ.∵PQ?平面ADPQ,∴CD⊥PQ,又∵CD∩DQ=D,∴PQ⊥平面DCQ.又PQ?平面PQC,所以平面PQC⊥平面DCQ.
(2)解 如图,以D为坐标原点,DA,DP,DC所在直线为x轴,y轴,z轴,建立空间直角坐标系D-xyz.
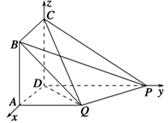
设AD=1,AB=m(m>0).
依题意有D(0,0,0),C(0,0,m),P(0,2,0),Q(1,1,0),B(1,0,m),则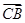 =(1,0,0),
=(1,0,0),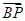 =(-1,2,-m),
=(-1,2,-m),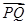 =(1,-1,0),
=(1,-1,0),
设n1=(x1,y1,z1)是平面PBC的法向量,则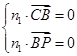 即
即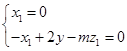
因此可取n1=(0,m,2).
设n2=(x2,y2,z2)是平面PBQ的法向量,则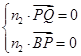 即
即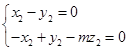
可取n2=(m,m,1).
又∵二面角Q-BP-C的余弦值为-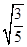 ,∴|cos 〈n1,n2〉|=|-
,∴|cos 〈n1,n2〉|=|-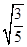 |.
|.
∴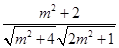 =
=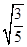 ,整理得m4+7m2-8=0.
,整理得m4+7m2-8=0.
又∵m>0,解得m=1.因此,所求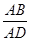 的值为1
的值为1
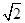 ,DP=2,又∵PD∥QA,∴∠PDQ=∠AQD=45°,在△DPQ中,由余弦定理可得PQ=
,DP=2,又∵PD∥QA,∴∠PDQ=∠AQD=45°,在△DPQ中,由余弦定理可得PQ=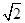 .
.∴DQ2+PQ2=DP2,∴PQ⊥DQ,又∵PD⊥平面ABCD,∴PD⊥DC,∵CD⊥DA,DA∩PD=D,∴CD⊥平面ADPQ.∵PQ?平面ADPQ,∴CD⊥PQ,又∵CD∩DQ=D,∴PQ⊥平面DCQ.又PQ?平面PQC,所以平面PQC⊥平面DCQ.
(2)解 如图,以D为坐标原点,DA,DP,DC所在直线为x轴,y轴,z轴,建立空间直角坐标系D-xyz.

设AD=1,AB=m(m>0).
依题意有D(0,0,0),C(0,0,m),P(0,2,0),Q(1,1,0),B(1,0,m),则
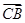 =(1,0,0),
=(1,0,0),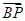 =(-1,2,-m),
=(-1,2,-m),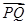 =(1,-1,0),
=(1,-1,0),设n1=(x1,y1,z1)是平面PBC的法向量,则
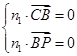 即
即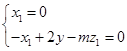
因此可取n1=(0,m,2).
设n2=(x2,y2,z2)是平面PBQ的法向量,则
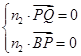 即
即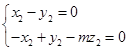
可取n2=(m,m,1).
又∵二面角Q-BP-C的余弦值为-
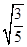 ,∴|cos 〈n1,n2〉|=|-
,∴|cos 〈n1,n2〉|=|-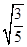 |.
|.∴
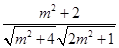 =
=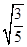 ,整理得m4+7m2-8=0.
,整理得m4+7m2-8=0.又∵m>0,解得m=1.因此,所求
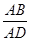 的值为1
的值为1
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
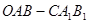 ,其中向量
,其中向量 ,三个向量之间的夹角均为
,三个向量之间的夹角均为 ,点
,点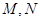 分别在
分别在 上且
上且 ,
,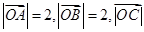 =4,如图
=4,如图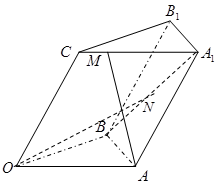
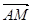 用向量
用向量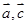 表示出来,并求
表示出来,并求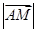 ;
;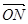 用
用 表示;
表示;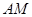 与
与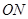 所成角的余弦值.
所成角的余弦值.
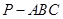 中,
中,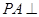 平面
平面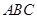 ,
,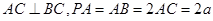 ,则
,则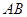 与平面
与平面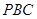 所成角的正弦值为__________.
所成角的正弦值为__________.
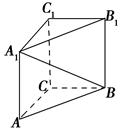
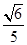
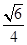
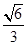
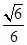
 ABC的重心,则
ABC的重心,则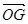 等于
等于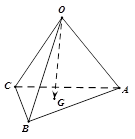


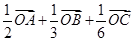
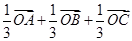
 、
、 、
、 ,则
,则 与
与 共线需满足( )
共线需满足( )



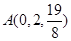 ,
,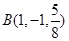 ,
,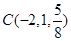 是平面
是平面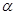 内的三点,设平面
内的三点,设平面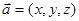 ,则
,则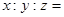 ______________
______________